
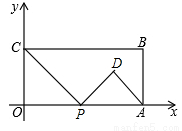
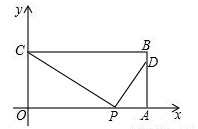
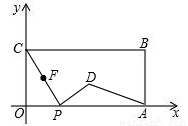
(本題14分)如圖,在平面直角坐標系中,矩形OABC的兩邊OA、OC分別在x軸、y軸的正半軸上,OA=4,OC=2.點P從點O出發,沿x軸以每秒1個單位長的速度向點A勻速運動,當點P到達點A時停止運動,設點P運動的時間是t秒.將線段CP的中點繞點P按順時針方向旋轉90°得點D,點D隨點P的運動而運動,連接DP、DA.
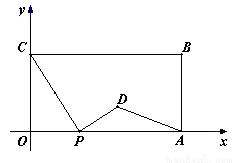
(1)請用含t的代數式表示出點D的坐標;
(2)求t為何值時,△DPA的面積最大,最大為多少?
(3)在點P從O向A運動的過程中,△DPA能否成為直角三角形?若能,求t的值.若不能,請說明理由;
(4)請直接寫出隨著點P的運動,點D運動路線的長.
(1)D(t+1,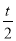 );(2)當t=2時,S最大=1;(3)能,2或3;(4)
);(2)當t=2時,S最大=1;(3)能,2或3;(4)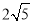 .
.
【解析】
試題分析:(1)設出P點坐標,再求出CP的中點坐標,根據相似的性質即可求出D點坐標;
(2)根據D點的坐標及三角形的面積公式直接求解即可;
(3)先判斷出可能為直角的角,再根據勾股定理求解;
(4)根據點D的運動路線與OB平行且相等解答即可.
試題解析:(1)∵點P從點O出發,沿x軸以每秒1個單位長的速度向點A勻速運動,∴OP=t,而OC=2,∴P(t,0),設CP的中點為F,則F點的坐標為(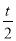 ,1),
,1),
∴將線段CP的中點F繞點P按順時針方向旋轉90°得點D,其坐標為(t+1,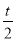 );
);
(2)∵D點坐標為(t+1,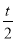 ),OA=4,∴S△DPA=
),OA=4,∴S△DPA=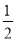 AP×
AP×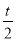 =
=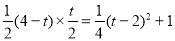 ,
,
∴當t=2時,S最大=1;
(3)能構成直角三角形.
①當∠PDA=90°時,PC∥AD,由勾股定理得,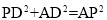 ,
,
即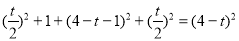 ,解得,t=2或t=-6(舍去).∴t=2秒.
,解得,t=2或t=-6(舍去).∴t=2秒.
②當∠PAD=90°時,此時點D在AB上,可知,△COP∽△PAD,
∴CP:PD=CO:PA,∴2:1=2:PA,PA=1,即t+1=4,t=3秒.
綜上,可知當t為2秒或3秒時,△DPA能成為直角三角形.
(4)∵根據點D的運動路線與OB平行且相等,OB=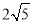 ,
,
∴點D運動路線的長為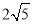 .
.
考點:1.二次函數的最值;2.待定系數法求一次函數解析式;3.直角三角形的性質;4.矩形的性質.


科目:初中數學 來源:2014-2015學年江蘇省泰興市九年級上學期期中考試數學試卷(解析版) 題型:解答題
(8分)如圖所示在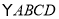 中,
中,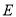 是
是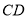 的延長線上一點,
的延長線上一點,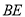 與
與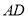 交于點
交于點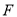 ,
,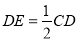 .
.
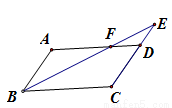
(1)求證: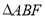 ∽
∽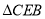 ;
;
(2)若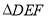 面積為2,求
面積為2,求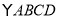 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年河北省沙河市九年級上學期期末模擬考試數學試卷(解析版) 題型:選擇題
已知拋物線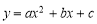 的開口向下,頂點坐標為(2,-3),那么該拋物線有( )
的開口向下,頂點坐標為(2,-3),那么該拋物線有( )
A.最大值 -3 B.最小值-3 C.最小值2 D.最大值2
查看答案和解析>>
科目:初中數學 來源:2014-2015學年河北省沙河市九年級上學期第二次月度聯考數學試卷(解析版) 題型:選擇題
已知兩圓的半徑分別是5和8,若兩圓相交,則兩圓的圓心距可以是( )
A.3 B.8 C.13 D.18
查看答案和解析>>
科目:初中數學 來源:2014-2015學年河北省沙河市九年級上學期第二次月度聯考數學試卷(解析版) 題型:選擇題
若拋物線y=x2-2x+c與y軸的交點為(0,-3)則該拋物線與x軸的交點是( )
A.(-1,0)和(0,3) B.(0,-1)和(3,0)
C.(-1,0)和(3,0) D.(0,-1)和(0,3)
查看答案和解析>>
科目:初中數學 來源:2014-2015學年河北省沙河市九年級上學期第四次月考數學試卷(解析版) 題型:選擇題
如圖,在直角坐標系中,正方形OABC的頂點O與原點重合,頂點A.C分別在x軸、y軸上,反比例函數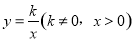 的圖象與正方形的兩邊AB、BC分別交于點M、N,ND⊥x軸,垂足為D,連接OM、ON、MN.下列結論:
的圖象與正方形的兩邊AB、BC分別交于點M、N,ND⊥x軸,垂足為D,連接OM、ON、MN.下列結論:
①△OCN≌△OAM;
②ON=MN;
③四邊形DAMN與△MON面積相等;
④若∠MON=450,MN=2,則點C的坐標為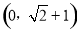 .
.
其中正確的個數是( )
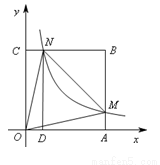
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中數學 來源:2014-2015學年福建省龍巖市九年級上學期半期考試數學試卷(解析版) 題型:解答題
(12分)已知x1,x2是一元二次方程2x2-2x+m+1=0的兩個實數根.
(1)求實數m的取值范圍;
(2)如果x1,x2滿足不等式7+4x1x2>x12+x22,且m為整數,求m的值.
查看答案和解析>>
科目:初中數學 來源:2013-2014學年湖北省咸寧市九年級上學期第二次月考數學試卷(解析版) 題型:選擇題
某班同學畢業時都將自己的照片向全班其他同學各送一張表示留念,全班共送1980張照片,如果全班有x名同學,根據題意,列出方程為( ).
A.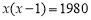 B.
B.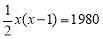
C.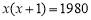 D.
D.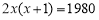
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com