Question

17．如圖，兩條互相平行的河岸，在河岸一邊測得AB為20米，在另一邊測得CD為70米，用測角器測得∠ACD=30°，測得∠BDC=45°，求兩條河岸之間的距離．（$\sqrt{2}≈1.4，\sqrt{3}$≈1.7，結果保留整數）

Answer 1

分析 分別過點A、B作CD的垂線交CD于點E、F，令兩條河岸之間的距離為h．則AE=BF=h，EF=AB=20．解Rt△ACE，得出CE=$\sqrt{3}$h，解Rt△BDF，求出DF=BF=h，根據CD=CE+EF+FD=70列出方程，求解即可．

解答 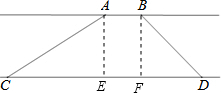解：如圖，分別過點A、B作CD的垂線交CD于點E、F，令兩條河岸之間的距離為h．
∵AE⊥CD，BF⊥CD，AB∥CD，AB=20，
∴AE=BF=h，EF=AB=20．
在Rt△ACE中，∵∠AEC=90°，∠ACE=30°，
∴tan∠ACE=$\frac{AE}{CE}$，即tan30°=$\frac{h}{CE}$，
∴CE=$\sqrt{3}$h．
在Rt△BDF中，∵∠BFD=90°，∠BDF=45°，
∴DF=BF=h．
∵CD=70，
∴CE+EF+FD=70，
∴$\sqrt{3}$h+20+h=70，
∴h=25（$\sqrt{3}$-1）≈18．
答：兩條河岸之間的距離約為18米．

點評 本題考查了解直角三角形的應用，通過作輔助線構造直角三角形，用含h的代數式分別表示出CE與FD是解題的關鍵．