
 如圖,AB是⊙O的直徑,∠ABT=45°,AT=AB
如圖,AB是⊙O的直徑,∠ABT=45°,AT=AB分析 (1)根據等腰直角三角形的性質求出∠BAT=90°,根據切線的判定定理證明即可;
(2)根據勾股定理求出TC的長;作CD⊥AT于D,根據平行線分線段成比例定理求出CD、AD的長,根據勾股定理計算即可.
解答 (1)證明:∵∠ABT=45°,AT=AB,
∴∠ATB=∠ABT=45°,
∴∠BAT=90°,
∴AT是⊙O的切線;
(2)解:∵⊙O的半徑是2,
∴AT=AB=4,
∵∠OAT=90°,
∴OT=$\sqrt{A{T}^{2}+O{A}^{2}}$=2$\sqrt{5}$,
∴TC=OT-OC=2$\sqrt{5}$-2,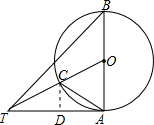 作CD⊥AT于D,
作CD⊥AT于D,
則AO∥CD,
∴$\frac{CD}{AO}$=$\frac{TC}{TO}$=$\frac{TD}{TA}$,即$\frac{CD}{2}$=$\frac{2\sqrt{5}-2}{2\sqrt{5}}$=$\frac{4-AD}{4}$,
解得,CD=$\frac{10-2\sqrt{5}}{5}$,AD=$\frac{4\sqrt{5}}{5}$,
由勾股定理得,AC2=CD2+AD2=$\frac{40-8\sqrt{5}}{5}$.
點評 本題考查的是切線的判定和平行線分線段成比例定理的應用,掌握經過半徑的外端且垂直于這條半徑的直線是圓的切線、靈活運用平行線分線段成比例定理是解題的關鍵.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,已知反比例函數y=$\frac{2}{x}$的圖象上有一組點B1,B2,…,Bn,它們的橫坐標依次增加1,且點B1橫坐標為1.“①,②,③…”分別表示如圖所示的三角形的面積,記S1=①-②,S2=②-③,…,則S7的值為$\frac{1}{56}$,S1+S2+…+Sn=$\frac{n}{n+1}$(用含n的式子表示).
如圖,已知反比例函數y=$\frac{2}{x}$的圖象上有一組點B1,B2,…,Bn,它們的橫坐標依次增加1,且點B1橫坐標為1.“①,②,③…”分別表示如圖所示的三角形的面積,記S1=①-②,S2=②-③,…,則S7的值為$\frac{1}{56}$,S1+S2+…+Sn=$\frac{n}{n+1}$(用含n的式子表示).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 過直線l外一點P用直尺和圓規作直線l的垂線的方法是:以點P為圓心,大于點P到直線l的距離長為半徑畫弧,交直線l于點A、B;分別以A、B為圓心,大于$\frac{1}{2}$AB長為半徑畫弧,兩弧交于點C.連結PC,則PC⊥AB.
過直線l外一點P用直尺和圓規作直線l的垂線的方法是:以點P為圓心,大于點P到直線l的距離長為半徑畫弧,交直線l于點A、B;分別以A、B為圓心,大于$\frac{1}{2}$AB長為半徑畫弧,兩弧交于點C.連結PC,則PC⊥AB.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 已知:如圖,E在△ABC的邊AC上,且∠AEB=∠ABC.
已知:如圖,E在△ABC的邊AC上,且∠AEB=∠ABC.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
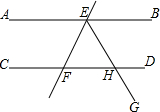 如圖,直線AB∥CD,直線EF分別交直線AB、CD于E、F,∠BEF的平分線EG交CD于H.若∠EFH=50°,則∠BEH的度數為( )
如圖,直線AB∥CD,直線EF分別交直線AB、CD于E、F,∠BEF的平分線EG交CD于H.若∠EFH=50°,則∠BEH的度數為( )| A. | 50° | B. | 55° | C. | 60° | D. | 65° |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com