
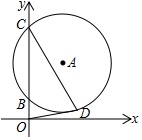 如圖,以點A(1,$\sqrt{3}$)為圓心的⊙A交y軸正半軸于B、C兩點,且OC=$\sqrt{3}$+1,點D是⊙A上第一象限內(nèi)的一點,連接OD、CD.若OD與⊙A相切,則CD的長為( )
如圖,以點A(1,$\sqrt{3}$)為圓心的⊙A交y軸正半軸于B、C兩點,且OC=$\sqrt{3}$+1,點D是⊙A上第一象限內(nèi)的一點,連接OD、CD.若OD與⊙A相切,則CD的長為( )| A. | $\sqrt{3}$-1 | B. | $\sqrt{3}$+1 | C. | 2$\sqrt{3}$ | D. | 2$\sqrt{2}$ |
分析 連接OA,連接AC,過點A作AE⊥OC于E,過點D作DF⊥CF交CA的延長線于F.首先證明△AOD為等腰直角三角形,在Rt△ADF,Rt△CDF中,解直角三角形即可解決問題.
解答 解:連接OA,連接AC,過點A作AE⊥OC于E,過點D作DF⊥CF交CA的延長線于F.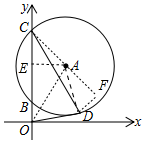
∵A(1,$\sqrt{3}$),
∴OA=$\sqrt{{1}^{2}+(\sqrt{3})^{2}}$=2,
∴CE=AE=1,AC=AD=$\sqrt{2}$
∴OD=$\sqrt{2}$,
∵AD=OD,∠ADO=90°,
∴△AOD為等腰直角三角形,
∴∠DAF=180°-45°-60°-45°=30°,
∴DF=$\frac{\sqrt{2}}{2}$,AF=$\frac{\sqrt{6}}{2}$,CF=$\sqrt{2}$+$\frac{\sqrt{6}}{2}$,
在Rt△CDF中,CD=$\sqrt{C{F}^{2}+D{F}^{2}}$=$\sqrt{(\sqrt{2}+\frac{\sqrt{6}}{2})^{2}+(\frac{\sqrt{2}}{2})^{2}}$=$\sqrt{3}$+1.
故選B.
點評 本題考查切線的性質(zhì)、坐標與圖形的性質(zhì)、等腰直角三角形的判定和性質(zhì)、30度的直角三角形的性質(zhì)等知識,解題的關(guān)鍵是學(xué)會填空常用輔助線,構(gòu)造特殊三角形解決問題,屬于中考常考題型.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數(shù)學(xué) 來源: 題型:填空題
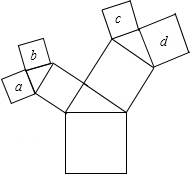 在如圖所示的圖形中,所有的四邊形都是正方形,所有的三角形都是直角三角形,若最大正方形的邊長為7cm,則正方形a,b,c,d的面積之和是147cm2.
在如圖所示的圖形中,所有的四邊形都是正方形,所有的三角形都是直角三角形,若最大正方形的邊長為7cm,則正方形a,b,c,d的面積之和是147cm2.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 向東走20千米與向西走15千米 | B. | 收入200元與虧損30元 | ||
| C. | 超過0.05mm與不足0.03mm | D. | 上升10米和下降7米 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com