Question

如圖所示，在平面直角坐標系中，雙曲線y=（x＜0）上有一點A（﹣2，2），AB⊥y軸于點B，點C是x軸正半軸上一動點，直線CB交雙曲線于點D，DE⊥x軸于點E，連接AE，AD，BE．

（1）當點C運動時，四邊形ADBE的形狀能變成菱形嗎？如果能，求出此時點C的位置，若不能，說明理由．

（2）小明經過探究發現：點C運動會影響四邊形ADBE形狀，但是AD與BE的位置關系始終不變，請你幫他解釋其中的原因．

Answer 1

【考點】反比例函數綜合題．

【分析】（1）若四邊形ADBE為菱形，則AB與DE互相垂直平分，則B和D的坐標可求得，然后利用待定系數法求得直線BC的解析式，進而求得C的坐標；

（2）設D的坐標是（a，﹣），利用利用待定系數法即可求利用a表示出AD和BE的解析式，根據直線平行的條件即可判斷．

【解答】解：（1）若四邊形ADBE為菱形，則AB與DE互相垂直平分，

由題意得，A（﹣2，2），B（0，2）．

則反比例函數的解析式是y=﹣，E（﹣1，0）D（﹣1，4）．

設直線BD的解析式是y=kx+b，

將B（0，2），D（﹣1，4）代入y=kx+b，可得：，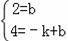

解得：，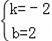

則直線BD的解析式是y=﹣2x+2，

所以C的坐標是（1，0）；

（2）設D的坐標是（a，﹣），直線AD的解析式是y=kx+b，則E（a，0）．

將A（﹣2，2），D（a，﹣）代入可得：，

解得：，

則直線AD的解析式是y=﹣x+（2﹣）．

同理可得直線BE的解析式是y=﹣x+2，

∴AD和BE始終平行．

【點評】本題考查了待定系數法求一次函數和直線的解析式，正確利用a表示出AD和BE的解析式是解決本題的關鍵．