

分析 先在Rt△MPN中,利用勾股定理,求得MN=13,再根據折疊的性質,得出BC=5+13+12=30,然后由直角三角形的面積公式,得到AB=$\frac{60}{13}$,進而求得矩形的面積.
解答 解:∵∠MPN=90°,PM=5,PN=12,
∴MN=13,BC=5+13+12=30.
根據直角三角形的面積公式,得
AB=$\frac{PM•PN}{MN}$=$\frac{60}{13}$,
∴矩形的面積=30×$\frac{60}{13}$=$\frac{1800}{13}$.
故矩形ABCD的面積為$\frac{1800}{13}$.
點評 此題綜合運用了勾股定理、折疊的性質和直角三角形的斜邊上的高等于兩直角邊的乘積除以斜邊的方法,本題難度適中.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
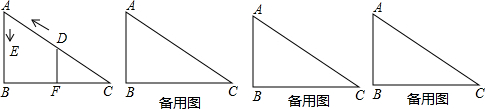
 如圖,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一點,將Rt△ABC沿CD折疊,使B點落在AC邊上的B′處,則∠CDB′等于( )
如圖,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一點,將Rt△ABC沿CD折疊,使B點落在AC邊上的B′處,則∠CDB′等于( )| A. | 40° | B. | 60° | C. | 70° | D. | 80° |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,PA,PB是⊙O的切線,A,B為切點,AC是⊙O的直徑.
如圖,PA,PB是⊙O的切線,A,B為切點,AC是⊙O的直徑.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com