
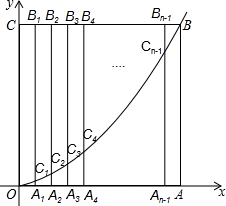
 如圖,邊長為n的正方形OABC的邊OA、OC分別在x軸和y軸的正半軸上,A1、A2、A3、…、An-1為OA的n等分點,B1、B2、B3、…Bn-1為CB的n等分點,連接A1B1、A2B2、A3B3、…、An-1Bn-1,分別交y=$\frac{1}{n}$x2(x≥0)于點C1、C2、C3、…、Cn-1,若有B5C5=3C5A5時,則n=10.
如圖,邊長為n的正方形OABC的邊OA、OC分別在x軸和y軸的正半軸上,A1、A2、A3、…、An-1為OA的n等分點,B1、B2、B3、…Bn-1為CB的n等分點,連接A1B1、A2B2、A3B3、…、An-1Bn-1,分別交y=$\frac{1}{n}$x2(x≥0)于點C1、C2、C3、…、Cn-1,若有B5C5=3C5A5時,則n=10. 分析 根據題意表示出OA5,B5A5的長,由B5C5=3C5A5確定點C5的坐標,代入解析式計算得到答案.
解答 解:∵正方形OABC的邊長為n,點A1,A2,…,An-1為OA的n等分點,點B1,B2,…,Bn-1為CB的n等分點,
∴OA5=$\frac{5}{n}$•n=5,A5B5=n,
∵B5C5=3C5A5,
∴C5(5,$\frac{n}{4}$),
∵點C5在y=$\frac{1}{n}$x2(x≥0)上,
∴$\frac{n}{4}$=$\frac{1}{n}$×52,
解得n=10.
故答案為:10.
點評 本題考查的是二次函數圖象上點的特征和正方形的性質,根據正方形的性質表示出點C5的坐標是解題的關鍵.


科目:初中數學 來源: 題型:選擇題
| A. | 0.1×10-8 | B. | 0.1×10-7 | C. | 1×10-8 | D. | 1×10-9 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知拋物線y=ax2+bx+3交x軸于A、B兩點(A在B左邊),交y軸于C點,且OC=3OA,對稱軸x=1交拋物線于D點.
如圖,已知拋物線y=ax2+bx+3交x軸于A、B兩點(A在B左邊),交y軸于C點,且OC=3OA,對稱軸x=1交拋物線于D點.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 函數y=x2+bx+c與y=x的圖象如圖所示,有以下結論:
函數y=x2+bx+c與y=x的圖象如圖所示,有以下結論:| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,一正方體包裝箱沿斜面坡角為30°的電梯上行,已知正方體包裝箱的棱長為2米,電梯AB長為16米,當正方體包裝箱的一個頂點到達電梯上端B時,求另一頂點C離地面的高度.(參考數據:$\sqrt{3}$≈1.73)
如圖,一正方體包裝箱沿斜面坡角為30°的電梯上行,已知正方體包裝箱的棱長為2米,電梯AB長為16米,當正方體包裝箱的一個頂點到達電梯上端B時,求另一頂點C離地面的高度.(參考數據:$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,直線OA過點(4,3),則tanα=( )
如圖,直線OA過點(4,3),則tanα=( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,在Rt△ABC中,∠ACB=90°,AB的垂直平分線DE交AC于E,交BC的延長線于F,若∠F=30°,BE=4,則AD的長是( )
如圖,在Rt△ABC中,∠ACB=90°,AB的垂直平分線DE交AC于E,交BC的延長線于F,若∠F=30°,BE=4,則AD的長是( )| A. | 4 | B. | 2 | C. | 6 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,在正方形ABCD中,△BCE是等邊三角形,連接BD交CE于點M,若AB=$\sqrt{3}$,則EM的長為( )
如圖,在正方形ABCD中,△BCE是等邊三角形,連接BD交CE于點M,若AB=$\sqrt{3}$,則EM的長為( )| A. | 3-$\sqrt{3}$ | B. | 2$\sqrt{3}$-3 | C. | 2-$\sqrt{3}$ | D. | $\sqrt{3}$-1 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com