
【題目】(1)如圖1,△ABC為等邊三角形,點D、E分別為邊AB、AC上的一點,將圖形沿線段DE所在的直線翻折,使點A落在BC邊上的點F處求證:![]() ;
;
(2)如圖2,按圖1的翻折方式,若等邊△ABC的邊長為4,當![]() 時,求
時,求![]() 的值;
的值;
(3)如圖3,在![]() 中,
中,![]() ,點D是AB邊上的中點,在BC的下方作射線BE,使得
,點D是AB邊上的中點,在BC的下方作射線BE,使得![]() ,點P是射線BE上一個動點,當
,點P是射線BE上一個動點,當![]() ,求BP的長.
,求BP的長.
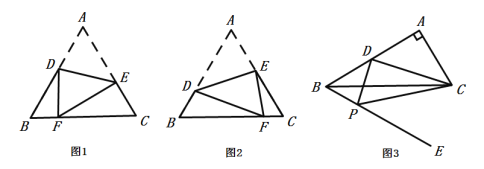
【答案】(1)見解析;(2)![]() ;(3)2或6
;(3)2或6
【解析】
(1)根據三角形外角的性質證明∠BDF=∠EFC,從而可得△BDF∽△CFE,根據相似三角形對應邊成比例即可得出結論;
(2)過D作DH⊥BC.設BF=x,則CF=4-x.設EF=2a,則DF=3a,AE=2a,BD=4-AD=4-3a,CE=4-AE=4-2a,由相似三角形對應邊成比例,即可得出x、a的值,從而求得BD、DF、DH的長,根據正弦的定義即可得出結論;
(3)解Rt△ABC得到BC、AB、BD的長.過C作CF⊥BC,交BE于F,解Rt△BCF,得到CF、BF的長.通過證明△DBPΔPFC,由相似三角形對應邊成比例即可得出結論.
(1)![]() ,
,
又![]() ,
,
![]() ,
,
![]() .
.
又![]() ,
,
![]() ,
,
![]() ,
,
即![]() .
.
(2)過D作![]() .
.
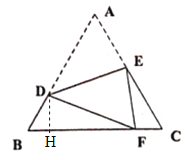
設![]() ,則
,則![]() .
.
設![]() ,則
,則![]() ,AE=2a,
,AE=2a,
![]() ,
,
![]() .
.
由(1)知![]() ,
,
![]() ,
,
即![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
(3)∵![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() .
.
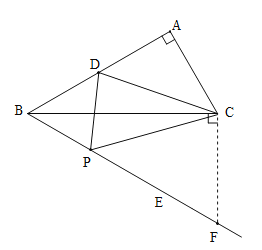
過C作![]() ,交BE于F.
,交BE于F.
∵∠CBF=30°,
∴![]() CF=BC=
CF=BC=![]() ,
,
∴CF=4,∴BF=2CF=8.
∵![]()
![]() ,
,
![]() .
.
∴![]() ,
,
又![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() 或6.
或6.


科目:初中數學 來源: 題型:
【題目】(本題8分)一個不透明的口袋中有四個完全相同的小球,它們分別標號為1,2,3,4
(1)隨機摸取一個小球,直接寫出“摸出的小球標號是3”的概率
(2)隨機摸取一個小球然后放回,再隨機摸出一個小球,直接寫出下列結果:
① 兩次取出的小球一個標號是1,另一個標號是2的概率
② 第一次取出標號是1的小球且第二次取出標號是2的小球的概率
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明同學利用寒假30天時間販賣草莓,了解到某品種草莓成本為10元/千克,在第![]() 天的銷售量與銷售單價如下(每天內單價和銷售量保持一致):
天的銷售量與銷售單價如下(每天內單價和銷售量保持一致):
銷售量 |
|
銷售單價 | 當 |
當 |
設第![]() 天的利潤
天的利潤![]() 元.
元.
(1)請計算第幾天該品種草莓的銷售單價為25元/千克?
(2)這30天中,該同學第幾天獲得的利潤最大?最大利潤是多少?注:利潤=(售價-成本)×銷售量
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著城市化建設的發展,交通擁堵成為上班高峰時難以避免的現象.為了解龍泉驛某條道路交通擁堵情況,龍泉某中學同學經實地統計分析研究表明:當![]() 時,車流速度v(千米/小時)是車流密度x(輛/千米)的一次函數.當該道路的車流密度達到220輛/千米時,造成堵塞,此時車流速度為0千米/小時;當車流密度為95輛/千米時,車流速度為50千米/小時.
時,車流速度v(千米/小時)是車流密度x(輛/千米)的一次函數.當該道路的車流密度達到220輛/千米時,造成堵塞,此時車流速度為0千米/小時;當車流密度為95輛/千米時,車流速度為50千米/小時.
(1)當![]() 時,求車流速度v(千米/小時)與車流密度x(輛/千米)的函數關系式;
時,求車流速度v(千米/小時)與車流密度x(輛/千米)的函數關系式;
(2)為使該道路上車流速度大于40千米/小時且小于60千米/小時,應控制該道路上的車流密度在什么范圍內?
(3)車流量(輛/小時)是單位時間內通過該道路上某觀測點的車輛數,即:車流量=車流速度×車流密度.當![]() 時,求該道路上車流量y的最大值.此時車流速度為多少?
時,求該道路上車流量y的最大值.此時車流速度為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知直線l1:y=kx+b 經過點A(﹣![]() ,0)和點B(2,5).
,0)和點B(2,5).
(1)求直線l1與y軸的交點坐標;
(2)若點C(a,a+2)與點D在直線l1上,過點D的直線l2與x軸正半軸交于點 E,當AC=CD=CE 時,求DE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,圖形都是由面積為1的正方形按一定的規律組成,其中,第(1)個圖形中面積為1的正方形有2個,第(2)個圖形中面積為1的正方形有5個,第(3)個圖形中面積為1的正方形有9個,按此規律,則第(6)個圖形中面積為1的正方形的個數為( )

A.14B.20C.24D.27
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解某校初三學生上周末使用手機的情況(選項:A.聊天;B.學習;C.購物;D.游戲;E.其他),隨機抽查了該校初三若干名學生,對其上周末使用手機的情況進行統計(每個學生只選一個選項),繪制了統計表和條形統計圖.
選項 | 人數 | 頻率 |
A | 15 | 0.3 |
B | 10 | m |
C | 5 | 0.1 |
D | n | |
E | 5 | 0.1 |
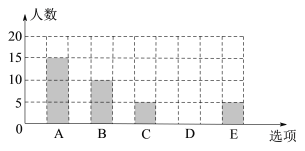
根據以上信息回答下列問題:
(1)這次調查的樣本容量是 ;
(2)統計表中m= ,n= ,補全條形統計圖;
(3)若該校初三有540名學生,請估計該校初三學生上周末利用手機學習的人數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com