
【題目】隨著城市化建設的發展,交通擁堵成為上班高峰時難以避免的現象.為了解龍泉驛某條道路交通擁堵情況,龍泉某中學同學經實地統計分析研究表明:當![]() 時,車流速度v(千米/小時)是車流密度x(輛/千米)的一次函數.當該道路的車流密度達到220輛/千米時,造成堵塞,此時車流速度為0千米/小時;當車流密度為95輛/千米時,車流速度為50千米/小時.
時,車流速度v(千米/小時)是車流密度x(輛/千米)的一次函數.當該道路的車流密度達到220輛/千米時,造成堵塞,此時車流速度為0千米/小時;當車流密度為95輛/千米時,車流速度為50千米/小時.
(1)當![]() 時,求車流速度v(千米/小時)與車流密度x(輛/千米)的函數關系式;
時,求車流速度v(千米/小時)與車流密度x(輛/千米)的函數關系式;
(2)為使該道路上車流速度大于40千米/小時且小于60千米/小時,應控制該道路上的車流密度在什么范圍內?
(3)車流量(輛/小時)是單位時間內通過該道路上某觀測點的車輛數,即:車流量=車流速度×車流密度.當![]() 時,求該道路上車流量y的最大值.此時車流速度為多少?
時,求該道路上車流量y的最大值.此時車流速度為多少?
【答案】(1)v=﹣![]() x+88;(2)70<x<120;(3)車流量y的最大值是每小時4840輛,此時車流速度是44千米/時.
x+88;(2)70<x<120;(3)車流量y的最大值是每小時4840輛,此時車流速度是44千米/時.
【解析】
(1)當20≤x≤220時,設車流速度v與車流密度x的函數關系式為v=kx+b,再根據待定系數法求解即可;
(2)由(1)的解析式建立不等式組求出其解集即可;
(3)設車流量y與x之間的關系式為y=vx,當20≤x≤220時表示出相應的二次函數關系,由二次函數的性質就可以求出結果.
解:(1)設車流速度v與車流密度x的函數關系式為v=kx+b,由題意,得
![]() ,解得:
,解得: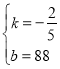 ,
,
∴當20≤x≤220時,v=﹣![]() x+88;
x+88;
(2)由題意,得: ,解得:70<x<120,
,解得:70<x<120,
∴應控制該道路上的車流密度在70<x<120范圍內;
(3)設車流量y與x之間的關系式為y=vx,
當20≤x≤220時,y=(﹣![]() x+88)x=﹣
x+88)x=﹣![]() (x﹣110)2+4840,
(x﹣110)2+4840,
∴當x=110時,y最大=4840,此時![]() 千米/時,
千米/時,
∴當車流密度是110輛/千米時,車流量y取得最大值是每小時4840輛,此時車流速度是44千米/時.


 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案科目:初中數學 來源: 題型:
【題目】在一個不透明的口袋里裝有只有顏色不同的黑、白兩種顏色的球共5只.某學習小組做摸球實驗,將球攪勻后從中隨機摸出一個球記下顏色,再把它放回袋中,不斷重復.下表是活動進行中的一組統計數據:
摸球的次數 n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次數 m | 58 | 96 | 116 | 295 | 484 | 601 |
摸到白球的頻率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
(1)請估計:當n很大時,摸到白球的頻率將會接近 (結果精確到0.1);
(2)試估算口袋中黑球有 只,白球有 只;
(3)在(2)的結論下,請你用列表或樹狀圖求出隨機摸出兩個球都是白球的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點E是邊長為2的正方形ABCD的邊BC上的一動點(不與端點重合),將△ABE沿AE翻折至△AFE的位置,若△CDF是等腰三角形,則BE=________.
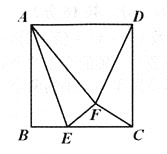
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某服裝店的員工與老板齊心協力,在2019年的經營中,每月的利潤都在不斷增加.該服裝店的老板每季度都讓員工總結經驗與不足,下面是策劃師與銷售![]() 品牌服裝的員工在第二季度總結的一部分.
品牌服裝的員工在第二季度總結的一部分.
策劃師的發言:第四月的利潤為50萬元,從第四月開始,第二季度的月增長率不變,第二季度的總利潤為182萬元.
銷售![]() 品牌的員工發言:銷售的
品牌的員工發言:銷售的![]() 品牌服裝在四月份中,進價為100元,售價為140元,每周銷售60件,由于該服裝進貨量少,因此,采用漲價銷售,每件漲1元時,平均每周少售2件,每周盈利2250元.
品牌服裝在四月份中,進價為100元,售價為140元,每周銷售60件,由于該服裝進貨量少,因此,采用漲價銷售,每件漲1元時,平均每周少售2件,每周盈利2250元.

請根據總結解答相關的問題:
(1)求第二季度月增長率;
(2)![]() 品牌服裝每周盈利2250元時,每件售價應該是多少元?
品牌服裝每周盈利2250元時,每件售價應該是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
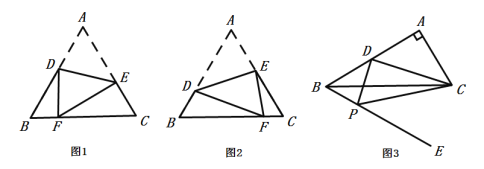
【題目】(1)如圖1,△ABC為等邊三角形,點D、E分別為邊AB、AC上的一點,將圖形沿線段DE所在的直線翻折,使點A落在BC邊上的點F處求證:![]() ;
;
(2)如圖2,按圖1的翻折方式,若等邊△ABC的邊長為4,當![]() 時,求
時,求![]() 的值;
的值;
(3)如圖3,在![]() 中,
中,![]() ,點D是AB邊上的中點,在BC的下方作射線BE,使得
,點D是AB邊上的中點,在BC的下方作射線BE,使得![]() ,點P是射線BE上一個動點,當
,點P是射線BE上一個動點,當![]() ,求BP的長.
,求BP的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知點M(n,﹣n )在第二象限,過點M的直線y=kx+b(0<k<1)分別交x軸、y軸于點A,B,過點M作MN⊥x軸于點N,則下列點在線段AN的是( )
A. ((k﹣1)n,0) B. ((k+![]() )n,0)) C. (
)n,0)) C. (![]() ,0) D. ((k+1)n,0)
,0) D. ((k+1)n,0)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,O是對角線AC的中點.將ABCD繞點B順時針旋轉90°.旋轉后的四邊形為A'B′C′D',點A,C,D,O的對應點分別為A′,C',D',O’,若AB=8,BC=10,則線段CO’的長為_____.
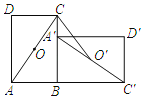
查看答案和解析>>
科目:初中數學 來源: 題型:
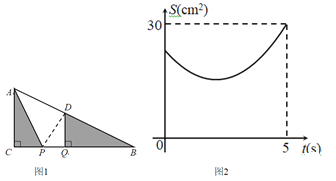
【題目】如圖1,在Rt△ABC中,∠ACB=90°,AC=6cm.點P、Q是BC邊上兩個動點(點Q在點P右邊),PQ=2cm,點P從點C出發,沿CB向右運動,運動時間為t秒.5s后點Q到達點B,點P、Q停止運動,過點Q作QD⊥BC交AB于點D,連接AP,設△ACP與△BQD的面積和為S(cm),S與t的函數圖像如圖2所示.
(1)圖1中BC= cm,點P運動的速度為 cm/s;
(2)t為何值時,面積和S最小,并求出最小值;
(3)連接PD,以點P為圓心線段PD的長為半徑作⊙P,當⊙P與![]() 的邊相切時,求t的值.
的邊相切時,求t的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com