
【題目】如圖,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,將
,將![]() 繞點
繞點![]() 順時針旋轉得到
順時針旋轉得到![]() ,點
,點![]() 、
、![]() 分別為
分別為![]() 、
、![]() 的中點,若點
的中點,若點![]() 剛好落在邊
剛好落在邊![]() 上,則
上,則![]() ______.
______.
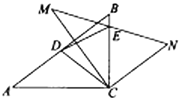
【答案】![]()
【解析】
根據旋轉性質及直角三角形斜邊中線等于斜邊一半,求出CD=CE=5,再根據勾股定理求DE長,![]() 的值即為等腰△CDE底角的正弦值,根據等腰三角形三線合一構建直角三角形求解.
的值即為等腰△CDE底角的正弦值,根據等腰三角形三線合一構建直角三角形求解.
如圖,過D點作DM⊥BC,垂足為M,過C作CN⊥DE,垂足為N,
在Rt△ACB中,AC=8,BC=6,由勾股定理得,AB=10,
∵D為AB的中點,
∴CD=![]() ,
,
由旋轉可得,∠MCN=90°,MN=10,
∵E為MN的中點,
∴CE=![]() ,
,
∵DM⊥BC,DC=DB,
∴CM=BM=![]() ,
,
∴EM=CE-CM=5-3=2,
∵DM=![]() ,
,
∴由勾股定理得,DE=![]() ,
,
∵CD=CE=5,CN⊥DE,
∴DN=EN=![]() ,
,
∴由勾股定理得,CN=![]() ,
,
∴sin∠DEC=![]() .
.

故答案為:![]() .
.


科目:初中數學 來源: 題型:
【題目】某運動會期間,甲、乙、丙三位同學參加乒乓球單打比賽,用抽簽的方式確定第一場比賽的人選.
(1)若已確定甲參加第一次比賽,求另一位選手恰好是乙同學的概率;
(2)用畫樹狀圖或列表的方法,寫出參加第一場比賽選手的所有可能,并求選中乙、丙兩位同學參加第一場比賽的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
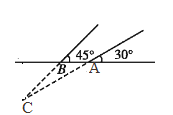
【題目】某煤礦發生瓦斯爆炸,該地救援隊立即趕赴現場進行救援,救援隊利用生命探測儀在地面A,B兩個探測點探測到C處有生命跡象.已知A,B兩點相距6米,探測線與地面的夾角分別是30°和45°,試確定生命所在點C的深度.(精確到0.1米,參考數據:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了掌握八年級數學考試卷的命題質量與難度系數,命題組教師赴外地選取一個水平相當的八年級班級進行預測,將考試成績分布情況進行處理分析,制成頻數分布表如下(成績得分均為整數):
組別 | 成績分組 | 頻數頻率 | 頻數 |
1 |
| 2 | 0.05 |
2 |
| 4 | 0.10 |
3 |
|
| 0.2 |
4 |
| 10 | 0.25 |
5 |
|
|
|
6 |
| 6 | 0.15 |
合計 | 40 | 1.00 |
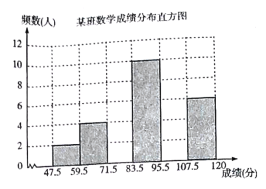
根據表中提供的信息解答下列問題:
(1)頻數分布表中的![]() ,
,![]() ,
,![]() ;
;
(2)已知全區八年級共有200個班(平均每班40人),用這份試卷檢測,108分及以上為優秀,預計優秀的人數約為 ,72分及以上為及格,預計及格的人數約為 ,及格的百分比約為 ;
(3)補充完整頻數分布直方圖.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市2017年對市區綠化工程投入的資金是5000萬元,為爭創全國文明衛生城,加大對綠化工程的投入,2019年投入的資金是7200萬元,且從2017年到2019年,兩年間每年投入資金的年平均增長率相同.
(1)求該市對市區綠化工程投入資金的年平均增長率;
(2)若投入資金的年平均增長率不變,那么該市在2020年預計需投入多少萬元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖為二次函數y=ax2+bx+c的圖象,在下列說法中①ac>0;②方程ax2+bx+c=0的根是x1=﹣1,x2=3;③a+b+c<0;④當x>1時,y隨x的增大而增大,正確的是( )
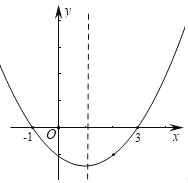
A. ①③B. ②④C. ①②④D. ②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有三個大小一樣的正六邊形,可按下列方式進行拼接:
方式1:如圖1;
方式2:如圖2;
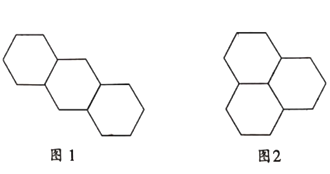
若有四個邊長均為1的正六邊形,采用方式1拼接,所得圖案的外輪廓的周長是_______.有![]() 個邊長均為1的正六邊形,采用上述兩種方式的一種或兩種方式混合拼接,若得圖案的外輪廓的周長為18,則
個邊長均為1的正六邊形,采用上述兩種方式的一種或兩種方式混合拼接,若得圖案的外輪廓的周長為18,則![]() 的最大值為__________.
的最大值為__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,在平面直角坐標系中,拋物線![]() 的對稱軸為直線
的對稱軸為直線![]() ,將直線
,將直線![]() 繞著點
繞著點![]() 順時針旋轉
順時針旋轉![]() 的度數后與該拋物線交于
的度數后與該拋物線交于![]() 兩點(點
兩點(點![]() 在點
在點![]() 的左側),點
的左側),點![]() 是該拋物線上一點
是該拋物線上一點
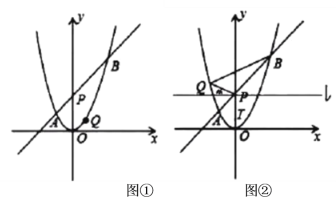
(1)若![]() ,求直線
,求直線![]() 的函數表達式
的函數表達式
(2)若點![]() 將線段分成
將線段分成![]() 的兩部分,求點
的兩部分,求點![]() 的坐標
的坐標
(3)如圖②,在(1)的條件下,若點![]() 在
在![]() 軸左側,過點
軸左側,過點![]() 作直線
作直線![]() 軸,點
軸,點![]() 是直線
是直線![]() 上一點,且位于
上一點,且位于![]() 軸左側,當以
軸左側,當以![]() ,
,![]() ,
,![]() 為頂點的三角形與
為頂點的三角形與![]() 相似時,求
相似時,求![]() 的坐標
的坐標
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com