
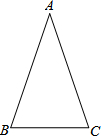
 如圖,在△ABC中,AB=AC,∠A=36°,且BC=2,則AB=$\sqrt{5}+1$.
如圖,在△ABC中,AB=AC,∠A=36°,且BC=2,則AB=$\sqrt{5}+1$. 分析 作∠ABC的平分線交AC于D如圖,根據(jù)等腰三角形的性質(zhì)和三角形內(nèi)角和定理可計(jì)算出∠ABC=∠C=72°,則∠ABD=∠CBD=36°,所以DA=DB,易得BD=BC,則AD=BC,再證明△BCD∽△ABC,得到BC2=CD•AD,則AD2=CD•AD,根據(jù)黃金分割的定義得到點(diǎn)D為AC的黃金分割點(diǎn),據(jù)此可得AB的長(zhǎng).
解答 解:如圖,作∠ABC的平分線交AC于D,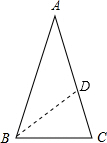
∵AB=AC,且∠A=36°,
∴∠ABC=∠C=72°,
∴∠ABD=∠CBD=36°,
∴DA=DB,
而∠BDC=∠A+∠ABD=72°,
∴BD=BC,
∴AD=BC,
∵∠CBD=∠A,∠BCD=∠ACB,
∴△BCD∽△ABC,
∴BC:AC=CD:BC,
∴BC2=CD•AD,
∴AD2=CD•AD,
∴點(diǎn)D為AC的黃金分割點(diǎn),
∴$\frac{AD}{AC}$=$\frac{BC}{AC}$=$\frac{\sqrt{5}-1}{2}$,
即$\frac{2}{AC}$=$\frac{\sqrt{5}-1}{2}$,
∴AC=$\sqrt{5}+1$=AB,
故答案為:$\sqrt{5}+1$.
點(diǎn)評(píng) 本題考查了黃金分割,解題時(shí)注意:若點(diǎn)C把線段AB分成兩條線段AC和BC(AC>BC),且使AC是AB和BC的比例中項(xiàng),點(diǎn)C叫做線段AB的黃金分割點(diǎn),其中AC=$\frac{\sqrt{5}-1}{2}$AB,線段AB的黃金分割點(diǎn)有兩個(gè).


 小學(xué)課堂作業(yè)系列答案
小學(xué)課堂作業(yè)系列答案 金博士一點(diǎn)全通系列答案
金博士一點(diǎn)全通系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 該函數(shù)的圖象經(jīng)過(guò)點(diǎn)(2,2) | B. | 該函數(shù)的圖象位于第一、三象限 | ||
| C. | 當(dāng)x>0時(shí),y的值隨x的增大而增大 | D. | 當(dāng)x>-1時(shí),y>4 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
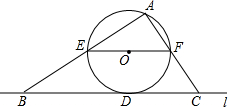 如圖,直線l與⊙相切于點(diǎn)D,過(guò)圓心O作EF∥l交⊙O于E、F兩點(diǎn),點(diǎn)A是⊙O上一點(diǎn),連接AE,AF,并分別延長(zhǎng)交直線于B、C兩點(diǎn);若⊙的半徑R=5,BD=12,則∠ACB的正切值為$\frac{7}{5}$.
如圖,直線l與⊙相切于點(diǎn)D,過(guò)圓心O作EF∥l交⊙O于E、F兩點(diǎn),點(diǎn)A是⊙O上一點(diǎn),連接AE,AF,并分別延長(zhǎng)交直線于B、C兩點(diǎn);若⊙的半徑R=5,BD=12,則∠ACB的正切值為$\frac{7}{5}$.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
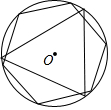 圖中的正三角形和正六邊形有公共的外接圓⊙O.則這個(gè)正三角形和正六邊形邊長(zhǎng)的比為( )
圖中的正三角形和正六邊形有公共的外接圓⊙O.則這個(gè)正三角形和正六邊形邊長(zhǎng)的比為( )| A. | $\sqrt{6}$:2 | B. | $\sqrt{3}$:2 | C. | $\sqrt{3}$:1 | D. | 2:1 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | ①② | B. | ①③ | C. | ①②③ | D. | ②③④ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com