Question

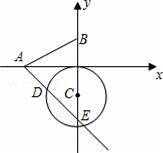
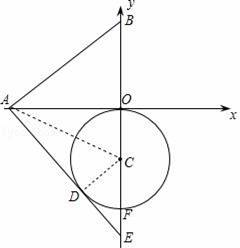
如圖，已知A、B兩點的坐標分別為（﹣2，0）、（0，1），⊙C 的圓心坐標為（0，﹣1），半徑為1．若D是⊙C上的一個動點，射線AD與y軸交于點E，則△ABE面積的最大值是（　　）

A．3       B．    C．    D．4

　

Answer 1

B【考點】切線的性質；三角形的面積．

【專題】計算題；壓軸題．

【分析】當射線AD與⊙C相切時，△ABE面積的最大．設EF=x，由切割線定理表示出DE，可證明△CDE∽△AOE，根據相似三角形的性質可求得x，然后求得△ABE面積．

【解答】解：當射線AD與⊙C相切時，△ABE面積的最大．

連接AC，

∵∠AOC=∠ADC=90°，AC=AC，OC=CD，

∴Rt△AOC≌Rt△ADC，

∴AD=AO=2，

連接CD，設EF=x，

∴DE²=EF•OE，

∵CF=1，

∴DE=，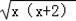

∴△CDE∽△AOE，

∴=，

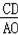
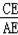
即=，

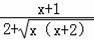
解得x=，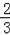

S_△ABE===．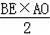

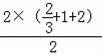
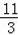
故選：B．

【點評】本題是一個動點問題，考查了切線的性質和三角形面積的計算，解題的關鍵是確定當射線AD與⊙C相切時，△ABE面積的最大．