已知一次函數的圖象經過點P（3，5），且平行于直線y=2x．
（1）求該一次函數的解析式；
（2）若點Q（x，y）在該直線上，且在x軸的下方，求x的取值范圍．
【考點】待定系數法求一次函數解析式；一次函數圖象上點的坐標特征．
【分析】（1）根據兩直線平行可知該一次函數斜率k=2，設出解析式，將點P坐標代入可得；
（2）根據直線上的點Q在x軸下方可得y＜0，解不等式可得x的范圍．
【解答】解：（1）∵一次函數的圖象平行于直線y=2x，可設該一次函數解析式為y=2x+b，
∴將點P（3，5）代入得：6+b=5，
解得：b=﹣1，
故一次函數解析式為：y=2x﹣1；
（2）∵點Q（x，y）在x軸下方，
∴y=2x﹣1＜0，
解得：x＜
．
【點評】本題主要考查一次函數解析式及圖象上的點的坐標，待定系數法求出解析式是前提，根據點的位置確定函數值小于0．
科目：初中數學 來源： 題型：
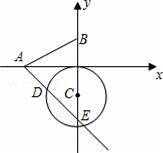
如圖，已知A、B兩點的坐標分別為（﹣2，0）、（0，1），⊙C 的圓心坐標為（0，﹣1），半徑為1．若D是⊙C上的一個動點，射線AD與y軸交于點E，則△ABE面積的最大值是（ ）
A．3 B．
C．
D．4
查看答案和解析>>
科目：初中數學 來源： 題型：
為了防控流感，某校積極進行校園環境消毒，購買了甲、乙兩種消毒液共100瓶。其中甲種6元／瓶，乙種9元／瓶。
（1）如果購買這兩種消毒液共用780元。求甲乙兩種消毒液各購買多少瓶？
（2）該校準備再次購買這兩種消毒液（不包括已經購買的100瓶），使乙種瓶數是甲種瓶數的2倍，且所需費用不超過1200元（不包括780元），則甲種消毒液最多能再買多少瓶？
查看答案和解析>>
科目：初中數學 來源： 題型：
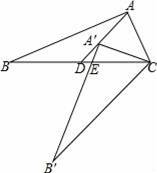
如圖，Rt△ABC中，∠BAC=90°，將△ABC繞點C逆時針旋轉，旋轉后的圖形是△A′B′C，點A的對應點A′落在中線AD上，且點A′是△ABC的重心，A′B′與BC相交于點E，那么BE：CE= ．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
有解，則a的取值范圍是（ ）
； 
cm，BC=2cm，CD=3cm，AD=5cm，求四邊形ABCD的面積。