
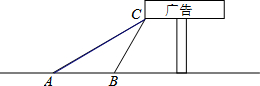
 如圖,某學校數學興趣小組想了解“第25屆世界技巧錦標賽倒計時”廣告牌的高度,他們在A點處測得廣告牌底端C點的仰角為30°,然后向廣告牌前進10m到達點B處,又測得C點的仰角為60°.請你根據以上數據求廣告牌底端C點離地面的高度.(結果保留根號)
如圖,某學校數學興趣小組想了解“第25屆世界技巧錦標賽倒計時”廣告牌的高度,他們在A點處測得廣告牌底端C點的仰角為30°,然后向廣告牌前進10m到達點B處,又測得C點的仰角為60°.請你根據以上數據求廣告牌底端C點離地面的高度.(結果保留根號) 分析 過C點作CD⊥AB于D,根據三角形外角的性質得出∠CBD=∠CAB+∠ACB,故可得出∠ACB=30°,BC=AB=10.在Rt△BCD中根據sin60°=$\frac{CD}{BC}$即可得出CD的長.
解答  解:過C點作CD⊥AB于D,
解:過C點作CD⊥AB于D,
∵∠CBD=∠CAB+∠ACB,
∴∠ACB=30°,
∴∠ACB=∠CAB,
∴BC=AB=10.
在Rt△BCD中,
sin60°=$\frac{CD}{BC}$,
∴CD=10×$\frac{\sqrt{3}}{2}$=5$\sqrt{3}$(m).
因此C點離地面的高度為5$\sqrt{3}$m.
點評 本題考查的是解直角三角形的應用-仰角俯角問題,根據題意作出輔助線,構造出直角三角形,利用銳角三角函數的定義求解是解答此題的關鍵.


科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
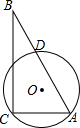 如圖,直角△ABC的直角頂點C,另一頂點A及斜邊AB的中點D都在⊙O上,已知:AC=6,BC=8,則⊙O的半徑為$\frac{25}{8}$.
如圖,直角△ABC的直角頂點C,另一頂點A及斜邊AB的中點D都在⊙O上,已知:AC=6,BC=8,則⊙O的半徑為$\frac{25}{8}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
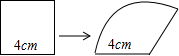 手工課上,小明將一個邊長為4cm的正方形鐵絲框,變形成為如圖所示一個扇形框,周長不變,且扇形框半徑等于正方形的邊長,則該扇形的面積大小為16cm2.
手工課上,小明將一個邊長為4cm的正方形鐵絲框,變形成為如圖所示一個扇形框,周長不變,且扇形框半徑等于正方形的邊長,則該扇形的面積大小為16cm2.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com