Question

20．如圖，在菱形ABCD中，∠B=120°，AD=10，AD的中點為P，AC上有動點Q，連接PQ，DQ，求PQ+DQ的最小值，并證明你的結論．

Answer 1

分析 連接BD，根據菱形的對角線平分一組對角線可得∠ABD=$\frac{1}{2}$∠ABC=60°，然后判斷出△ABD是等邊三角形，連接PB，根據軸對稱確定最短路線問題，PB與AC的交點Q即為所求的點Q，QP+QD的最小值=PB，然后根據等邊三角形的性質求出PB即可得解．

解答 ①解：如圖1，連接BD、PB．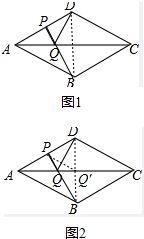
∵四邊形ABCD是菱形，
∴∠ABD=$\frac{1}{2}$∠ABC=$\frac{1}{2}$×120°=60°，
∵AB=AD（菱形的鄰邊相等），
∴△ABD是等邊三角形，
∵B、D關于對角線AC對稱，圖1
∴PB與AC的交點Q即為所求的點Q，PQ+QD的最小值=PB，
∵P是AD的中點，
∴PB⊥AD，
∵AD=10，
∴PB=$\frac{\sqrt{3}}{2}$×10=5$\sqrt{3}$．
②證明：如圖2，在線段AC上取一點異于點Q的點Q′，連接PQ′、BQ′．
在△Q′PB中，∵Q′P+Q′B＞PB
∴Q′P+Q′B＞PQ+QB，
∵B、D關于直線AC對稱，圖2
∴QD=BQ，
∴Q′P+Q′B＞QP+QD
∴QP+QD最小．

點評 本題考查了軸對稱確定最短路線問題、菱形的性質、等邊三角形的判定與性質以及三角形的邊角之間關系，熟記性質與最短路線的確定方法找出點P的位置是解題的關鍵．