

分析 (1)由∠BAC=∠EDF=60°,推出△ABC、△DEF為等邊三角形,于是得到∠BCE+∠ACE=∠DCA+∠ECA=60°,推出△BCE≌△ACD(SAS),根據(jù)全等三角形的性質(zhì)得到AD=BE,即可得到結(jié)論;
(2)在FA上截取FM=AE,連接DM,推出△AED≌△MFD(SAS),根據(jù)全等三角形的性質(zhì)得到DA=DM=AB=AC,∠ADE=∠MDF,證得∠ADM=∠EDF=∠BAC,推出△ABC≌△DAM(SAS),根據(jù)全等三角形的性質(zhì)得到AM=BC,即可得到結(jié)論.
解答 證明:(1)∵∠BAC=∠EDF=60°,
∴△ABC、△DEF為等邊三角形,
∴∠BCE+∠ACE=∠DCA+∠ECA=60°,
在△BCE和△ACD中$\left\{\begin{array}{l}BC=AC\\∠BCE=∠ACD\\ CE=CD\end{array}\right.$
∴△BCE≌△ACD(SAS),
∴AD=BE,
∴AE+AD=AE+BE=AB=AF;
(2)在FA上截取FM=AE,連接DM,
∵∠BAC=∠EDF,
∴∠AED=∠MFD,
在△AED和△MFD中
$\left\{\begin{array}{l}{AE=MF}\\{∠AKD=∠MFD}\\{KD=FD}\end{array}\right.$
∴△AED≌△MFD(SAS),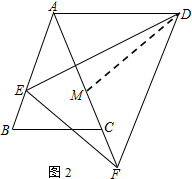
∴DA=DM=AB=AC,∠ADE=∠MDF,
∴∠ADE+∠EDM=∠MDF+∠EDM,
即∠ADM=∠EDF=∠BAC,
在△ABC和△DAM中,$\left\{\begin{array}{l}{AB=DA}\\{∠BAC=∠ADM}\\{AC=DM}\end{array}\right.$,
∴△ABC≌△DAM(SAS),
∴AM=BC,
∴AE+BC=FM+AM=AF.
即AF=AE+BC.
點(diǎn)評(píng) 本題考查了全等三角形的判定和性質(zhì),等腰三角形的性質(zhì),等邊三角形的性質(zhì),正確的作出輔助線是解題的關(guān)鍵.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
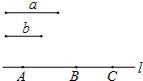 尺規(guī)作圖:如圖,已知線段a,b.
尺規(guī)作圖:如圖,已知線段a,b.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
 (1)如圖,點(diǎn)C在線段AB上,AC=8cm,CB=6cm,點(diǎn)M、N分別是AC、BC的中點(diǎn),求線段MN的長(zhǎng);
(1)如圖,點(diǎn)C在線段AB上,AC=8cm,CB=6cm,點(diǎn)M、N分別是AC、BC的中點(diǎn),求線段MN的長(zhǎng);查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
 如圖,在Rt△ABC中,∠C=90°,AC=12,BC=9,AB的垂直平分線分別交AB、AC于點(diǎn)D、E.求:
如圖,在Rt△ABC中,∠C=90°,AC=12,BC=9,AB的垂直平分線分別交AB、AC于點(diǎn)D、E.求:查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 火車(chē)開(kāi)到月球上 | B. | 拋出的石子會(huì)下落 | ||
| C. | 明天臨海會(huì)下雨 | D. | 早晨的太陽(yáng)從東方升起 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
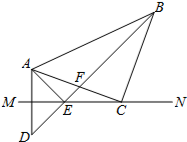 如圖,已知,MN是AD的垂直平分線,點(diǎn)C在MN上,∠MCA=20°,∠ACB=90°,CA=CB=5,BD交MN于點(diǎn)E,交AC于點(diǎn)F,連接AE.
如圖,已知,MN是AD的垂直平分線,點(diǎn)C在MN上,∠MCA=20°,∠ACB=90°,CA=CB=5,BD交MN于點(diǎn)E,交AC于點(diǎn)F,連接AE. 查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
 如圖,是一塊四邊形綠地的示意圖,其中AB長(zhǎng)為24米,BC長(zhǎng)15米,CD長(zhǎng)為20米,DA長(zhǎng)7米,∠C=90°,求綠地ABCD的面積.
如圖,是一塊四邊形綠地的示意圖,其中AB長(zhǎng)為24米,BC長(zhǎng)15米,CD長(zhǎng)為20米,DA長(zhǎng)7米,∠C=90°,求綠地ABCD的面積.查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com