

分析 (1)先根據(jù)∠AOC:∠COD:∠DOB=5:3:4,設(shè)∠AOC=5x,∠COD=3x,∠DOB=4x,再根據(jù)∠AOC+∠COD+∠BOD=120°,列出方程5x+3x+4x=120°,求得x的值后,得出∠AOC=50°,∠COD=30°,∠DOB=40°,再根據(jù)∠MON=∠DOM+∠CON-∠COD進(jìn)行計(jì)算,即可∠MON的度數(shù);
(2)先根據(jù)OM平分∠AOD,ON平分∠BOC,得出∠DOM=$\frac{1}{2}$∠AOD,∠CON=$\frac{1}{2}$∠BOC,再根據(jù)∠MON=∠DOM+∠CON-∠COD=$\frac{1}{2}$∠AOD+$\frac{1}{2}$∠BOC-∠COD=$\frac{1}{2}$(∠AOD+∠BOC)-∠COD=$\frac{1}{2}$(∠AOB+∠COD)-∠COD進(jìn)行計(jì)算,即可得出∠MON的度數(shù).
解答  解:(1)如圖1,∵∠AOC:∠COD:∠DOB=5:3:4,
解:(1)如圖1,∵∠AOC:∠COD:∠DOB=5:3:4,
∴可設(shè)∠AOC=5x,∠COD=3x,∠DOB=4x,
∵∠AOB=120°,
∴∠AOC+∠COD+∠BOD=120°,
∴5x+3x+4x=120°,
解得x=10°,
∴∠AOC=50°,∠COD=30°,∠DOB=40°,
∵OM平分∠AOD,ON平分∠BOC,
∴∠DOM=$\frac{1}{2}$∠AOD=$\frac{1}{2}$(50°+30°)=40°,
∠CON=$\frac{1}{2}$∠BOC=$\frac{1}{2}$(30°+40°)=35°,
∴∠MON=∠DOM+∠CON-∠COD=40°+35°-30°=45°;
(2)如圖2,∵OM平分∠AOD,ON平分∠BOC,
∴∠DOM=$\frac{1}{2}$∠AOD,∠CON=$\frac{1}{2}$∠BOC,
∴∠MON=∠DOM+∠CON-∠COD
=$\frac{1}{2}$∠AOD+$\frac{1}{2}$∠BOC-∠COD
=$\frac{1}{2}$(∠AOD+∠BOC)-∠COD
=$\frac{1}{2}$(∠AOB+∠COD)-∠COD
=$\frac{1}{2}$∠AOB-$\frac{1}{2}$∠COD
=$\frac{1}{2}$×120°-$\frac{1}{2}$×30°
=45°.
點(diǎn)評(píng) 本題主要考查了角的計(jì)算以及角平分線的定義的運(yùn)用,解決問題的關(guān)鍵是根據(jù)角的和差關(guān)系進(jìn)行計(jì)算求解,其難點(diǎn)在于將∠MON用∠DOM+∠CON-∠COD進(jìn)行表示,解題時(shí)注意:從一個(gè)角的頂點(diǎn)出發(fā),把這個(gè)角分成相等的兩個(gè)角的射線叫做這個(gè)角的平分線.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
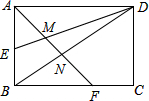 如圖,矩形ABCD的邊長AD=3,AB=2,E為AB的中點(diǎn),F(xiàn)在邊BC上,且BF=2FC,AF分別與DE,DB相交于點(diǎn)M,N.
如圖,矩形ABCD的邊長AD=3,AB=2,E為AB的中點(diǎn),F(xiàn)在邊BC上,且BF=2FC,AF分別與DE,DB相交于點(diǎn)M,N.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
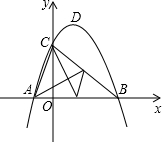 如圖,已知拋物線y=ax2+bx+3與x軸交于A,B兩點(diǎn)(A,B分別在原點(diǎn)的左右兩側(cè)),與y軸交于點(diǎn)C,拋物線的頂點(diǎn)為點(diǎn)D,且OA:OB:OC=1:3:3,求拋物線的解析式及頂點(diǎn)D的坐標(biāo).
如圖,已知拋物線y=ax2+bx+3與x軸交于A,B兩點(diǎn)(A,B分別在原點(diǎn)的左右兩側(cè)),與y軸交于點(diǎn)C,拋物線的頂點(diǎn)為點(diǎn)D,且OA:OB:OC=1:3:3,求拋物線的解析式及頂點(diǎn)D的坐標(biāo).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
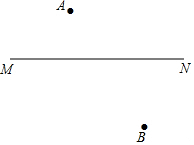 A、B為直線MN外兩點(diǎn),且在MN異側(cè),A、B到MN的距離不相等,試求一點(diǎn)P,滿足下條件:
A、B為直線MN外兩點(diǎn),且在MN異側(cè),A、B到MN的距離不相等,試求一點(diǎn)P,滿足下條件:查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com