
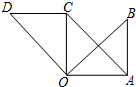
 如圖,在Rt△OAB中,∠OAB=90°,OA=AB=6,把△OAB繞點O沿逆時針方向旋轉90°,得到△OCD,連結AC.
如圖,在Rt△OAB中,∠OAB=90°,OA=AB=6,把△OAB繞點O沿逆時針方向旋轉90°,得到△OCD,連結AC.分析 (1)根據旋轉的性質得AB=CD,∠AOC=90°,∠OCD=∠OAB=90°,則可判斷OA∥CD,加上OA=AB,所以OA=CD,于是可判斷四邊形OACD是平行四邊形;
(2)直接根據平行四邊形的面積公式計算.
解答 (1)證明:∵△OAB繞點O沿逆時針方向旋轉90°,得到△OCD,
∴AB=CD,∠AOC=90°,∠OCD=∠OAB=90°,
∴∠AOC=∠OCD,
∴OA∥CD,
又∵OA=AB,
∴OA=CD,
∴四邊形OACD是平行四邊形;
(2)四邊形OACD的面積=OA•OC=6×6=36.
點評 本題考查了旋轉的性質:對應點到旋轉中心的距離相等;對應點與旋轉中心所連線段的夾角等于旋轉角;旋轉前、后的圖形全等.也考查了平行四邊形的判定與性質.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | x-3<y-3 | B. | x+5>y+5 | C. | $\frac{x}{3}$<$\frac{y}{3}$ | D. | -2x>-2y |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | a=5,b=6 | B. | a=1,b=-6 | C. | a=-1,b=-6 | D. | a=5,b=-6 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
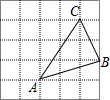 如圖,每個小方格都是邊長為1個單位的小正方形,A,B,C三點都是格點(每個小方格的頂點叫格點).
如圖,每個小方格都是邊長為1個單位的小正方形,A,B,C三點都是格點(每個小方格的頂點叫格點).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com