
| A. | 甲體育生此次射擊成績的眾數為7環 | |
| B. | 乙體育生此次射擊成績的平均數為7環 | |
| C. | 甲體育生此次射擊成績的成績比乙體育生的穩定 | |
| D. | 乙體育生此次射擊成績的中位數為6環 |
分析 根據方差、眾數、平均數和中位數的定義分別對每一項進行分析,即可得出答案.
解答 解:A、∵在甲設計測試中,7出現了3次,出現的次數最多,∴甲體育生此次射擊成績的眾數為7環,故本選項正確;
B、乙體育生此次射擊成績的平均數為(6+5+9+7+8)÷5=7環,故本選項正確;
C、∵甲體育生此次射擊成績的平均數是:(8+6+7+7+7)÷5=7(環),
∴甲體育生此次射擊成績的方差是:$\frac{1}{5}$[(8-7)2+(6-7)2+(7-7)2+(7-7)2+(7-7)2]=$\frac{2}{5}$,
∵乙體育生此次射擊成績的平均數是7環,
∴乙的方差是:S2=$\frac{1}{5}$[(6-7)2+(5-7)2+(9-7)2+(7-7)2+(8-7)2]=2,
∴甲體育生此次射擊成績的成績比乙體育生的穩定;
故本選項正確;
D、把乙體育生此次射擊成績從小到大排列為5,6,7,8,9,最中間的數是7,則乙體育生此次射擊成績的中位數為7環,故本選項錯誤;
故選D.
點評 本題考查了方差、眾數、平均數和中位數的定義.用到的知識點:一般地設n個數據,x1,x2,…xn的平均數為$\overline{x}$,則方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2];一組數據中出現次數最多的數據叫做這組數據的眾數.將一組數據按照從小到大(或從大到小)的順序排列,如果數據的個數是奇數,則處于中間位置的數就是這組數據的中位數;如果這組數據的個數是偶數,則中間兩個數據的平均數就是這組數據的中位數.


科目:初中數學 來源: 題型:解答題
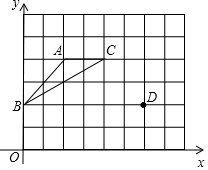 如圖,在坐標系的第一象限建立網格,網格中的每個小正方形邊長都為1,格點△ABC的頂點坐標分別為A(2,4)、B(0,2)、C(4,4).
如圖,在坐標系的第一象限建立網格,網格中的每個小正方形邊長都為1,格點△ABC的頂點坐標分別為A(2,4)、B(0,2)、C(4,4).查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 340+$\frac{2}{5}$ | B. | 340×(1+$\frac{2}{5}$) | C. | 340+340×$\frac{3}{5}$ | D. | 340×$\frac{2}{5}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,AB=3cm,BC=20cm,動點P從D點開始沿DA以2cm/s的速度向A運動,動點Q從B點開始沿BC以1cm/s的速度向C運動,P、Q分別從D、B同時出發,當其中一點到端點時,另一點也隨之停止運動,連結PQ,設運動時間為t.
如圖,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,AB=3cm,BC=20cm,動點P從D點開始沿DA以2cm/s的速度向A運動,動點Q從B點開始沿BC以1cm/s的速度向C運動,P、Q分別從D、B同時出發,當其中一點到端點時,另一點也隨之停止運動,連結PQ,設運動時間為t.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 5元 | B. | 4元 | C. | 3.5元 | D. | 3元 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
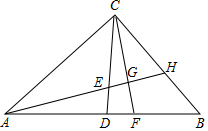 如圖,在△ABC中,∠ACB=90°,AC=BC,AB=4cm,CD是中線,點E、F同時從點D出發,以相同的速度分別沿DC、DB方向移動,當點E到達點C時,運動停止,直線AE分別與CF、BC相交于G、H,則在點 E、F移動過程中,點G移動路線的長度為( )
如圖,在△ABC中,∠ACB=90°,AC=BC,AB=4cm,CD是中線,點E、F同時從點D出發,以相同的速度分別沿DC、DB方向移動,當點E到達點C時,運動停止,直線AE分別與CF、BC相交于G、H,則在點 E、F移動過程中,點G移動路線的長度為( )| A. | 2 | B. | π | C. | 2 | D. | $\frac{{\sqrt{2}}}{2}$π |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com