
 如圖,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,AB=3cm,BC=20cm,動點P從D點開始沿DA以2cm/s的速度向A運動,動點Q從B點開始沿BC以1cm/s的速度向C運動,P、Q分別從D、B同時出發,當其中一點到端點時,另一點也隨之停止運動,連結PQ,設運動時間為t.
如圖,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,AB=3cm,BC=20cm,動點P從D點開始沿DA以2cm/s的速度向A運動,動點Q從B點開始沿BC以1cm/s的速度向C運動,P、Q分別從D、B同時出發,當其中一點到端點時,另一點也隨之停止運動,連結PQ,設運動時間為t.分析 (1)根據題意得:BQ=t,DP=2t,則CQ=20-t,AP=24-2t,與梯形面積公式得出方程,解方程求出t的值,則BQ=2,AP=20,作QM⊥AD于M,由勾股定理求出PQ即可;
(2)作CE⊥AD于E,則四邊形ABCE是矩形,得出AE=BC=20,CE=AB=3,∴DE=AD-AE=4,由勾股定理求出CD=5,分三種情況:
①DP=DC=5時,t=$\frac{5}{2}$s;
②CP=CD=5時,PE=DE=4,得出DP=8,即可求出t值;
③PC=PD時,P為CD的垂直平分線與AD的交點,證明△PDF∽△CDE,得出對應邊成比例求出DP,即可得出t的值.
解答 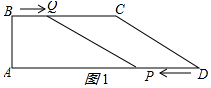 解:(1)存在,理由如下:如圖1所示:
解:(1)存在,理由如下:如圖1所示:
根據題意得:BQ=t,DP=2t,則CQ=20-t,AP=24-2t,
若線段PQ把梯形分成面積相等的兩部分,
則梯形ABQP的面積=梯形CDPQ的面積,
∴$\frac{1}{2}$(t+24-2t)×3=$\frac{1}{2}$(20-t+2t)×3,
解得:t=2,
∴BQ=2,AP=20,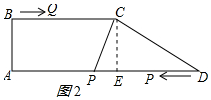
作QM⊥AD于M,則四邊形ABQM是矩形,
∴AM=BQ=2,QM=AB=3,
∴PM=AP-AM=20-2=18,
∴PQ=$\sqrt{P{M}^{2}+Q{M}^{2}}$=$\sqrt{1{8}^{2}+{3}^{2}}$=3$\sqrt{37}$;
∴存在線段PQ把梯形分成面積相等的兩部分,此時t=2s,PQ=3$\sqrt{37}$;
(2)作CE⊥AD于E,則四邊形ABCE是矩形,
∴AE=BC=20,CE=AB=3,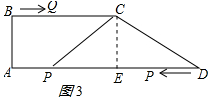
∴DE=AD-AE=4,
∴CD=$\sqrt{C{E}^{2}+D{E}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
分三種情況:①DP=DC=5時,如圖2所示:
則t=$\frac{5}{2}$s;
②CP=CD=5時,如圖3所示:
則PE=DE=4,
∴DP=8,∴t=8÷2=4(s);
③PC=PD時,P為CD的垂直平分線與AD的交點,如圖4所示: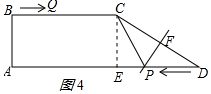
則DF=$\frac{5}{2}$,
∵∠CED=∠PFD=90°,∠D=∠D,
∴△PDF∽△CDE,
∴$\frac{DF}{DE}=\frac{DP}{DC}$,即$\frac{\frac{5}{2}}{4}=\frac{DP}{5}$,DP=$\frac{25}{8}$,
∴t=$\frac{25}{8}$÷2=$\frac{25}{16}$;
綜上所述:在P、Q運動過程中,△PCD能成為等腰三角形,t的值為$\frac{5}{2}$s或4s或$\frac{25}{16}$s.
點評 本題考查了梯形的性質、勾股定理、矩形的判定與性質、等腰三角形的判定、相似三角形的判定與性質以及分類討論思想的運用;熟練掌握梯形的性質和勾股定理是解決問題的關鍵.


 勵耘書業暑假銜接寧波出版社系列答案
勵耘書業暑假銜接寧波出版社系列答案科目:初中數學 來源: 題型:選擇題
| A. | $\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=0.5}\\{y=-7}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=5}\\{y=-2}\end{array}\right.$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
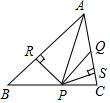 如圖,已知△ABC中,AQ=PQ、PR=PS、PR⊥AB于R,PS⊥AC于S,有以下三個結論:①AS=AR;②QP∥AR;③△BRP≌△CSP,其中( )
如圖,已知△ABC中,AQ=PQ、PR=PS、PR⊥AB于R,PS⊥AC于S,有以下三個結論:①AS=AR;②QP∥AR;③△BRP≌△CSP,其中( )| A. | 全部正確 | B. | 僅①正確 | C. | 僅①、②正確 | D. | 僅①、③正確 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 甲體育生此次射擊成績的眾數為7環 | |
| B. | 乙體育生此次射擊成績的平均數為7環 | |
| C. | 甲體育生此次射擊成績的成績比乙體育生的穩定 | |
| D. | 乙體育生此次射擊成績的中位數為6環 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
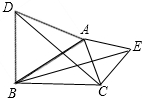 已知:如圖,△ABD和△ACE均為等腰三角形,且∠DAB=∠CAE=60°,則△ADC≌△AEB的根據是( )
已知:如圖,△ABD和△ACE均為等腰三角形,且∠DAB=∠CAE=60°,則△ADC≌△AEB的根據是( )| A. | SSS | B. | SAS | C. | ASA | D. | AAS |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com