
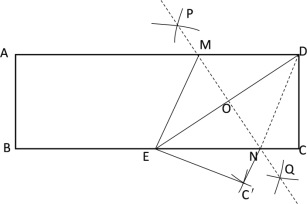
【題目】已知,如圖:長方形ABCD中,點E為BC邊的中點,將D折起,使點D落在點E處.

(1)請你用尺規作圖畫出折痕和折疊后的圖形.(不要求寫已知,求作和作法,保留作圖痕跡)
(2)若折痕與AD、BC分別交于點M、N,與DE交于點O,求證△MDO≌△NEO.
【答案】(1)圖見解析;(2)證明見解析
【解析】
(1)作DE的垂直平分線分別交AD和BC于點M、N,MN即為折痕,再以E為圓心,CD的長為半徑作弧,以N為圓心,NC的長為半徑作弧,兩弧交于點C′,四邊形MEC′N即為四邊形MDCN折疊后的圖形;
(2)根據矩形的性質可得AD∥BC,從而得出∠MDO=∠NEO,然后根據垂直平分線的定義可得DO=EO,最后利用ASA即可證出結論.
解:(1)分別以D、E為圓心,大于![]() DE的長為半徑作弧,兩弧分別交于點P、Q,連接PQ,分別交AD和BC于點M、N,連接ME和DN,此時MN垂直平分DE,MN即為折痕;
DE的長為半徑作弧,兩弧分別交于點P、Q,連接PQ,分別交AD和BC于點M、N,連接ME和DN,此時MN垂直平分DE,MN即為折痕;
再以E為圓心,CD的長為半徑作弧,以N為圓心,NC的長為半徑作弧,兩弧交于點C′,四邊形MEC′N即為四邊形MDCN折疊后的圖形;
(2)∵四邊形ABCD為矩形
∴AD∥BC
∴∠MDO=∠NEO
∵MN垂直平分DE
∴DO=EO
在△MDO和△NEO中
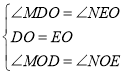
∴△MDO≌△NEO


 沖刺100分1號卷系列答案
沖刺100分1號卷系列答案 期末好成績系列答案
期末好成績系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知菱形ABCD的對角線相交于點O,延長AB至點E,使BE=AB,連結CE.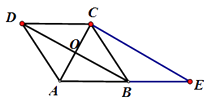
(1)求證:BD=EC;
(2)若AC=2, ![]() , 求菱形ABCD的面積.
, 求菱形ABCD的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用正方形硬紙板做三棱柱盒子,每個盒子由3個矩形側面和2個正三角形底面組成,硬紙板以如圖兩種方法裁剪(裁剪后邊角料不再利用)
A方法:剪6個側面;
B方法:剪4個側面和5個底面.

現有38張硬紙板,裁剪時x張用A方法,其余用B方法.
(1)用x的代數式分別表示裁剪出的側面和底面的個數;
(2)若裁剪出的側面和底面恰好全部用完,則能做多少個盒子?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形![]() 中,
中,![]() ,
,![]() 是
是![]() 的中點,將
的中點,將![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 后,點
后,點![]() 落在
落在![]() 的延長線上點
的延長線上點![]() 處,點
處,點![]() 落在點
落在點![]() 處.再將線段
處.再將線段![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() 得線段
得線段![]() ,連接
,連接![]() ,
,![]() .
.
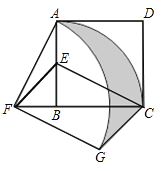
(1)求證:![]() ;
;
(2)求點![]() ,點
,點![]() 在旋轉過程中形成的
在旋轉過程中形成的![]() ,
,![]() 與線段
與線段![]() 所圍成的陰影部分的面積.
所圍成的陰影部分的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖1,在△ABC中,AD、BD分別平分∠BAC和∠ABC,AD、BD相交于點D,過點D作DE∥AC,DF∥BC分別交AB于點E、F.
①若∠EDF=80°,則∠ADB=________°;
②若∠C=![]() 則∠ADB=________°.
則∠ADB=________°.
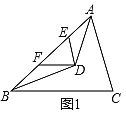
(2)如圖2,在△ABC中,若∠BAD=![]() ∠BAC,∠ABD=
∠BAC,∠ABD=![]() ∠ABC,AD、BD相交于點D,過點D作DE∥AC,DF∥BC分別交AB于點E、F,若∠EDF=60°,則∠ADB=_______°;
∠ABC,AD、BD相交于點D,過點D作DE∥AC,DF∥BC分別交AB于點E、F,若∠EDF=60°,則∠ADB=_______°;
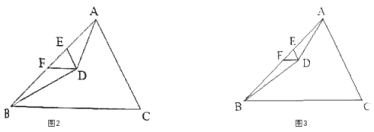
(3)如圖3,在△ABC中,AD、BD分別是∠BAC、∠ABC的![]() 等分線,AD、BD相交于點D,若∠BAD=
等分線,AD、BD相交于點D,若∠BAD=![]() ∠BAC,∠ABD=
∠BAC,∠ABD=![]() ∠ABC,過點D作DE∥AC,DF∥BC分別交AB于點E、F,若∠EDF=
∠ABC,過點D作DE∥AC,DF∥BC分別交AB于點E、F,若∠EDF=![]() ,則∠ADB的度數是多少?(用
,則∠ADB的度數是多少?(用![]() 表示)
表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖OA平分∠BAC,∠1=∠2.
求證:AO⊥BC.
同學甲說:要作輔助線;
同學乙說:要應用角平分線性質定理來解決:
同學丙說:要應用等腰三角形“三線合一”的性質定理來解決.
請你結合同學們的討論寫出證明過程.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】位于張家界核心景區的賀龍銅像,是我國近百年來最大的銅像.銅像由像體AD和底座CD兩部分組成.如圖,在Rt△ABC中,∠ABC=70.5°,在Rt△DBC中,∠DBC=45°,且CD=2.3米,求像體AD的高度(最后結果精確到0.1米,參考數據:sin70.5°≈0.943,cos70.5°≈0.334,tan70.5°≈2.824) 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】文美書店決定用不多于20000元購進甲乙兩種圖書共1200本進行銷售.甲、乙兩種圖書的進價分別為每本20元、14元,甲種圖書每本的售價是乙種圖書每本售價的1.4倍,若用1680元在文美書店可購買甲種圖書的本數比用1400元購買乙種圖書的本數少10本.
(1)甲乙兩種圖書的售價分別為每本多少元?
(2)書店為了讓利讀者,決定甲種圖書售價每本降低3元,乙種圖書售價每本降低2元,問書店應如何進貨才能獲得最大利潤?(購進的兩種圖書全部銷售完.)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com