
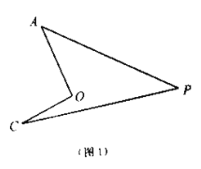
【題目】已知:如圖OA平分∠BAC,∠1=∠2.
求證:AO⊥BC.
同學甲說:要作輔助線;
同學乙說:要應用角平分線性質定理來解決:
同學丙說:要應用等腰三角形“三線合一”的性質定理來解決.
請你結合同學們的討論寫出證明過程.

科目:初中數學 來源: 題型:
【題目】給定關于 ![]() 的二次函數
的二次函數 ![]() ,
,
學生甲:當 ![]() 時,拋物線與
時,拋物線與 ![]() 軸只有一個交點,因此當拋物線與
軸只有一個交點,因此當拋物線與 ![]() 軸只有一個交點時,
軸只有一個交點時, ![]() 的值為3;
的值為3;
學生乙:如果拋物線在 ![]() 軸上方,那么該拋物線的最低點一定在第二象限;
軸上方,那么該拋物線的最低點一定在第二象限;
請判斷學生甲、乙的觀點是否正確,并說明你的理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
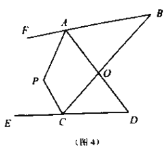
【題目】某游樂場部分平面圖如圖所示,C、E、A在同一直線上,D、E、B在同一直線上,測得A處與E處的距離為80 米,C處與D處的距離為34米,∠C=90°,∠ABE=90°,∠BAE=30°.( ![]() ≈1.4,
≈1.4, ![]() ≈1.7)
≈1.7)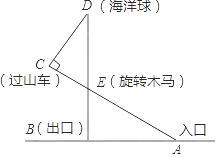
(1)求旋轉木馬E處到出口B處的距離;
(2)求海洋球D處到出口B處的距離(結果保留整數).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖:長方形ABCD中,點E為BC邊的中點,將D折起,使點D落在點E處.

(1)請你用尺規作圖畫出折痕和折疊后的圖形.(不要求寫已知,求作和作法,保留作圖痕跡)
(2)若折痕與AD、BC分別交于點M、N,與DE交于點O,求證△MDO≌△NEO.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,Rt△ABC的三個頂點分別是A(-3,2),B(0,4),C(0,2).
(1)將△ABC以點C為旋轉中心旋轉180°,畫出旋轉后對應的△A1B1C;平移△ABC,若點A的對應點A2的坐標為(0,-4),畫出平移后對應的△A2B2C2;
(2)若將△A1B1C繞某一點旋轉可以得到△A2B2C2 , 請直接寫出旋轉中心的坐標;
(3)在x軸上有一點P,使得PA+PB的值最小,請直接寫出點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀:已知a+b=﹣4,ab=3,求a2+b2的值.
解:∵a+b=﹣4,ab=3,
∴a2+b2=(a+b)2﹣2ab=(﹣4)2﹣2×3=10.
請你根據上述解題思路解答下面問題:
(1)已知a﹣b=﹣3,ab=﹣2,求(a+b)(a2﹣b2)的值.
(2)已知a﹣c﹣b=﹣10,(a﹣b)c=﹣12,求(a﹣b)2+c2的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在□ABCD中,∠DAB的平分線交CD于E點,且DE=5,EC=8.

(1)求□ABCD的周長;
(2)連結AC,若AC=12,求□ABCD的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知直線![]() ,把
,把![]() 的直角三角板
的直角三角板![]() 的直角頂點
的直角頂點![]() 放在直線
放在直線![]() 上.將直角三角板
上.將直角三角板![]() 在平面內繞點
在平面內繞點![]() 任意轉動,若轉動的過程中,直線
任意轉動,若轉動的過程中,直線![]() 與直線
與直線![]() 的夾角為60°,則
的夾角為60°,則![]() 的度數為___.
的度數為___.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】提出問題:
(1)如圖,我們將圖(1)所示的凹四邊形稱為“鏢形”.在“鏢形”圖中,![]() 與
與![]() 、
、![]() 、
、![]() 的數量關系為____.
的數量關系為____.
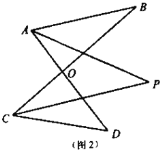
(2)如圖(2),已知![]() 平分
平分![]() ,
,![]() ,
,![]() ,求
,求![]() 的度數.
的度數.
由(1)結論得:![]()
所以![]() 即
即![]()
因為![]()
![]()
所以![]()
所以![]() .
.
解決問題:
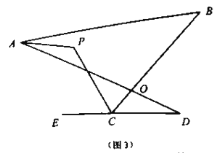
(1)如圖(3),直線![]() 平分
平分![]() ,
, ![]() 平分
平分![]() 的外角
的外角![]() ,猜想
,猜想![]() 與
與![]() 、
、![]() 的數量關系是______;
的數量關系是______;
(2)如圖(4),直線![]() 平分
平分![]() 的外角
的外角![]() ,
, ![]() 平分
平分![]() 的外角
的外角![]() ,猜想
,猜想![]() 與
與![]() 、
、![]() 的數量關系,并說明理由.
的數量關系,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com