
【題目】如圖,在平面直角坐標系中,一次函數的圖象y1=kx+b與反比例函數![]() 的圖象交于點A(1,5)和點B(m,1).
的圖象交于點A(1,5)和點B(m,1).
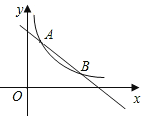
(1)求m的值和反比例函數的解析式;
(2)當x>0時,根據圖象直接寫出不等式![]() ≥kx+b的解集;
≥kx+b的解集;
(3)若經過點B的拋物線的頂點為A,求該拋物線的解析式.
【答案】(1)m的值為5,比例函數的解析式為![]() ;
;
(2)不等式![]() ≥kx+b的解集為0<x≤1或x≥5;
≥kx+b的解集為0<x≤1或x≥5;
(3)該拋物線的解析式是![]() .
.
【解析】試題分析:(1)把點A(1,5)代入y2=![]() ,求得n=5,再把 B(m,1)代入y2=
,求得n=5,再把 B(m,1)代入y2=![]() 得m=5,
得m=5,
再把A(1,5)、B(5,1)代入y1=kx+b, 即可得解;
(2)根據函數圖象及交點坐標即可求解;
(3)設二次函數的解析式為設拋物線的解析式為![]() ,把B(5,1)代入解析式即可得解.
,把B(5,1)代入解析式即可得解.
試題解析:(1)∵反比例函數![]() 的圖象交于點A(1,5),
的圖象交于點A(1,5),
∴5=n,即n=5,
∴y2=![]() ,
,
∵點B(m,1)在雙曲線上.
∴1=![]() ,
,
∴m=5,
∴B(5,1);
(2)不等式![]() ≥kx+b的解集為0<x≤1或x≥5;
≥kx+b的解集為0<x≤1或x≥5;
(3)∵拋物線的頂點為A(1,5),
∴設拋物線的解析式為![]() ,
,
∵拋物線經過B(5,1),
∴![]() ,解得
,解得![]() .
.
∴![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,□ABCD繞點A逆時針旋轉32°,得到□AB′C′D′,若點B′與點B是對應點,若點B′恰好落在BC邊上,則∠C=( ) 
A.106°
B.146°
C.148°
D.156°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市為解決部分市民冬季集中取暖問題需鋪設一條長3000米的管道,為盡量減少施工對交通造成的影響,實施施工時“…”,設實際每天鋪設管道x米,則可得方程 ![]() ,根據此情景,題中用“…”表示的缺失的條件應補為( )
,根據此情景,題中用“…”表示的缺失的條件應補為( )
A.每天比原計劃多鋪設10米,結果延期15天才完成
B.每天比原計劃少鋪設10米,結果延期15天才完成
C.每天比原計劃多鋪設10米,結果提前15天才完成
D.每天比原計劃少鋪設10米,結果提前15天才完成
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市的出租車的起步價為10元(行駛不超過3千米),以后每增加1千米,加價1.8元,現在某人乘出租車行駛P千米的路程(P>3)所需費用是( )
A.10+1.8P
B.1.8P
C.10﹣1.8P
D.10+1.8(P﹣3)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,小明在大樓30米高(即PH=30米)的窗口P處進行觀測,測得山坡上A處的俯角為15°,山腳B處的俯角為60°,已知該山坡的坡度i(即tan∠ABC)為1:![]() ,點P、H、B、C、A在同一個平面上.點H、B、C在同一條直線上,且PH⊥HC.
,點P、H、B、C、A在同一個平面上.點H、B、C在同一條直線上,且PH⊥HC.
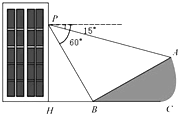
(1)山坡坡角(即∠ABC)的度數等于 度;
(2)求山坡A、B兩點間的距離(結果精確到0.1米).
(參考數據:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法正確的有( )
⑴若ac=bc,則a=b;
⑵若 ![]() ,則a=﹣b;
,則a=﹣b;
⑶若x2=y2 , 則﹣4ax2=﹣4by2;
⑷若方程2x+5a=11﹣x與6x+3a=22的解相同,則a的值為0.
A.4
B.3
C.2
D.1
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com