
 如圖,直線AB與⊙O相切于點A,AC、CD是⊙O的兩條弦,且CD∥AB,若⊙O的半徑為$\frac{5}{2}$,CD=4,則弦AC的長為( )
如圖,直線AB與⊙O相切于點A,AC、CD是⊙O的兩條弦,且CD∥AB,若⊙O的半徑為$\frac{5}{2}$,CD=4,則弦AC的長為( )| A. | 2$\sqrt{5}$ | B. | 3$\sqrt{2}$ | C. | 4 | D. | 2$\sqrt{3}$ |
分析 首先連接AO并延長,交CD于點E,連接OC,由直線AB與⊙O相切于點A,根據切線的性質,可得AE⊥AB,又由CD∥AB,可得AE⊥CD,然后由垂徑定理與勾股定理,求得OE的長,繼而求得AC的長.
解答 解:連接AO并延長,交CD于點E,連接OC,
∵直線AB與⊙O相切于點A,
∴EA⊥AB,
∵CD∥AB,
∠CEA=90°,
∴AE⊥CD,
∴CE=$\frac{1}{2}$CD=$\frac{1}{2}$×4=2,
∵在Rt△OCE中,OE=$\sqrt{O{C}^{2}-C{E}^{2}}$=$\frac{3}{2}$,
∴AE=OA+OE=4,
∴在Rt△ACE中,AC=$\sqrt{C{E}^{2}+A{E}^{2}}$=2$\sqrt{5}$.
故選A.
點評 此題考查了切線的性質、垂徑定理、勾股定理以及平行線的性質.此題難度適中,正確的添加輔助線是解題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,若有理數a、b在數軸上的對應點的位置如圖所示,則下列各式錯誤的是( )
如圖,若有理數a、b在數軸上的對應點的位置如圖所示,則下列各式錯誤的是( )| A. | $\frac{|a|}{a}$+$\frac{|b|}{b}$=0 | B. | a+b<0 | C. | |a+b|-a=b | D. | -b<a<-a<b |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
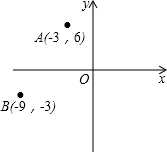 如圖,在平面直角坐標系中,已知點A(-3,6),B(-9,-3),以原點O為位似中心,相似比為$\frac{1}{3}$,把△ABO縮小,則點A的對應點A′的坐標是(-1,2)或(1,-2).
如圖,在平面直角坐標系中,已知點A(-3,6),B(-9,-3),以原點O為位似中心,相似比為$\frac{1}{3}$,把△ABO縮小,則點A的對應點A′的坐標是(-1,2)或(1,-2).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 陽光下,小亮測量“望月閣”的高AB.(如圖),由于觀測點與“望月閣”底部間的距離不易測得,因此他首先在直線BM上點C處固定平放一平面鏡,在鏡面上做了一個標記,小亮看著鏡面上的標記,他來回走動,走到點D時,看到“望月閣”頂端點A在鏡面中的像與鏡面上的標記重合,這時,測得小亮眼睛與地面的高度ED=1.5米,CD=2米.然后,在陽光下,他們用測影長的方法進行了第二次測量,方法如下:小亮從D點沿DM方向走了16米,到達“望月閣”影子的末端F點處,此時,測得小亮身高FG的影長FH=2.5米,FG=1.65米.已知AB⊥BM,ED⊥BM,GF⊥BM,其中,測量時所使用的平面鏡的厚度忽略不計,請你根據題中提供的相關信息,求出“望月閣”的高AB的長度.
陽光下,小亮測量“望月閣”的高AB.(如圖),由于觀測點與“望月閣”底部間的距離不易測得,因此他首先在直線BM上點C處固定平放一平面鏡,在鏡面上做了一個標記,小亮看著鏡面上的標記,他來回走動,走到點D時,看到“望月閣”頂端點A在鏡面中的像與鏡面上的標記重合,這時,測得小亮眼睛與地面的高度ED=1.5米,CD=2米.然后,在陽光下,他們用測影長的方法進行了第二次測量,方法如下:小亮從D點沿DM方向走了16米,到達“望月閣”影子的末端F點處,此時,測得小亮身高FG的影長FH=2.5米,FG=1.65米.已知AB⊥BM,ED⊥BM,GF⊥BM,其中,測量時所使用的平面鏡的厚度忽略不計,請你根據題中提供的相關信息,求出“望月閣”的高AB的長度.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com