【答案】
分析:法一:根據絕對值的性質,分x≥0和x<0兩種情況去掉絕對值號,然后分別對x
2-4x+3和x
2+4x+3分解因式,根據同號得正、異號得負求解.
法二:或者先分解因式求出|x|的解集,然后再解不等式組的解集.
解答:解:法一:
原不等式化為①
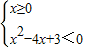
或②
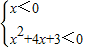
,(6分)
∵x
2-4x+3=(x-1)(x-3),x
2+4x+3=(x+1)(x+3),
∴解①得,1<x<3,解②得,-3<x<-1,(10分)
所以,原不等式的解為:1<x<3或-3<x<-1;(12分)
法二:原不等式化為:|x|
2+3<4|x|,
即(|x|-1)(|x|-3)<0,
∴1<|x|<3,
∴原不等式的解為-3<x<-1或1<x<3.
點評:本題分解因式后利用兩數相乘,同號得正、異號得負求解;也可以先求出|x|的范圍,再根據絕對值的性質去掉絕對值號,從而得到不等式的解集,這對初中生要求比較高,但只要平時學習的扎實,相信也是不難解決的.

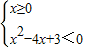 或②
或②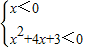 ,(6分)
,(6分)

