
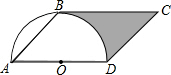
 如圖,已知?ABCD,∠A=45°,AD=4,以AD為直徑的半圓O與BC相切于點B,則圖中陰影部分的面積為6-π(結果保留π).
如圖,已知?ABCD,∠A=45°,AD=4,以AD為直徑的半圓O與BC相切于點B,則圖中陰影部分的面積為6-π(結果保留π). 分析 連接OB,求出OB=OA=OD=$\frac{1}{2}$AD=2,由S陰影部分=S?ABCD-SRt△AOB-S扇形BOD即可得出結果.
解答 解:連接OB,如圖所示: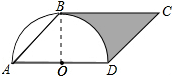
∵半圓O與BC相切于點B,
∴OB⊥BC,
∵四邊形ABCD為平行四邊形,
∴BO⊥AD,
∵AD=4,
∴OB=OA=OD=$\frac{1}{2}$AD=2,
∴S陰影部分=S?ABCD-SRt△AOB-S扇形BOD
=4×2-$\frac{1}{2}$×2×2-$\frac{1}{4}π$×22
=6-π.
故答案為:6-π.
點評 此題考查了平行四邊形的性質、切線的性質、平行四邊形面積與三角形面積以及扇形面積的計算等知識;把不規則圖形的面積轉化為規則圖形的面積是解決問題的關鍵.


 走進文言文系列答案
走進文言文系列答案科目:初中數學 來源: 題型:解答題
 如圖,線段MN表示一段高架道路,線段AB表示高架道路旁的一排居民樓.已知點A到MN的距離為15m,BA的延長線與MN相交于點D,且∠BDN=30°.若汽車沿著從M到N的方向在MN上行駛,方圓39m以內會受到噪音的影響,當其到達點P時,噪音開始影響這一排的居民樓;當其到達點Q時,它與這一排居民樓的距離為39m,求PQ的長度(精確到1m)(參考數據:$\sqrt{3}$≈1.7)
如圖,線段MN表示一段高架道路,線段AB表示高架道路旁的一排居民樓.已知點A到MN的距離為15m,BA的延長線與MN相交于點D,且∠BDN=30°.若汽車沿著從M到N的方向在MN上行駛,方圓39m以內會受到噪音的影響,當其到達點P時,噪音開始影響這一排的居民樓;當其到達點Q時,它與這一排居民樓的距離為39m,求PQ的長度(精確到1m)(參考數據:$\sqrt{3}$≈1.7)查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
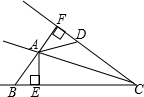 如圖,AC平分∠BCD,AB=AD,AE⊥BC于E,AF⊥CD于F.
如圖,AC平分∠BCD,AB=AD,AE⊥BC于E,AF⊥CD于F.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
| y | … | 8 | 3 | 0 | -1 | 0 | m | 8 | … |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,P為等邊△ABC內一點,PA=2,PB=1,PC=$\sqrt{3}$,則△ABC的面積為$\frac{7\sqrt{3}}{4}$.
如圖,P為等邊△ABC內一點,PA=2,PB=1,PC=$\sqrt{3}$,則△ABC的面積為$\frac{7\sqrt{3}}{4}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com