
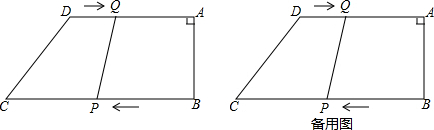
分析 (1)過點Q作QM⊥BC,分別求出AQ和BP的長,在Rt△QPM中,根據(jù)勾股定理得出QP的長即可;
(2)D、Q兩點的縱坐標相同,P、C兩點的縱坐標相同,四點在同一拋物線上說明它們的對稱軸是一樣的,寫出四點的坐標,再分別求出它們的對稱軸即可得解;
(3)先求出AQ、BP的長,根據(jù)圓外切四邊形的對邊和相等以及勾股定理進行解答,據(jù)此即可得解.
解答 解:(1)如圖1,過點Q作QM⊥BC,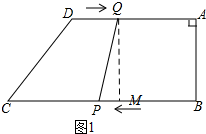 ∵在直角梯形ABCD中,AD∥BC,∠A=90°,
∵在直角梯形ABCD中,AD∥BC,∠A=90°,
∴四邊形ABMQ是矩形,
∴QM=AB=12,
當t=6時,DQ=6,AQ=16-6=10,BP=3×6=18,
∴BM=AQ=10,
∴PM=18-10=8,
在Rt△PQM中,∠PMQ=90°,PM=8,QM=12,
QP=$\sqrt{{8}^{2}+1{2}^{2}}$=$\sqrt{208}$=4$\sqrt{13}$;
(2)如圖2所示,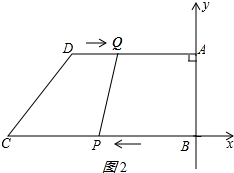
DQ=t,AQ=16-t,BP=3t,BC=21,AD=16,
∴D(-16,12),Q(t-16,12),C(-21,0),P(-3t,0),
D、Q兩點的對稱軸為:$\frac{-16+t-16}{2}$,
C、P兩點的對稱軸為:$\frac{-21-3t}{2}$,
∵D、Q、P、C四點在同一拋物線上,
∴$\frac{-16+t-16}{2}=\frac{-21-3t}{2}$,
解得:t=$\frac{11}{4}$;
當t=$\frac{11}{4}$時,D、Q、P、C四點在同一拋物線上;
(3)如圖3,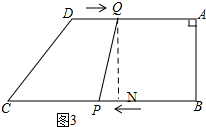 過點Q作QN⊥BC,垂足為N,
過點Q作QN⊥BC,垂足為N,
∵在直角梯形ABCD中,AD∥BC,∠A=90°,
∴四邊形ABNQ是矩形,
∴QN=AB=12,BN=AQ=16-t,BP=3t,
∵四邊形ABPQ為圓外切四邊形,
∴AQ+BP=PQ+AB,
∴PQ=16-t+3t-12=2t+4,PN=3t-(16-t)=4t-16,
在Rt△PNQ中,PQ2=PN2+QN2,
即:(2t+4)2=(4t-16)2+122,
解得:t=4或t=8(舍).
∴當t=4時,四邊形ABPQ為圓外切四邊形.
點評 本題是四邊形綜合題目,主要考查了動點問題、勾股定理、圓的外切四邊形的對邊和相等等知識點;認真分析題意,在第三問中認識到點P在7秒后停止是解題的關(guān)鍵,要注意認真總結(jié).


科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
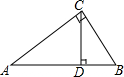 在直角三角形ABC中,∠ACB=90°,∠A、∠B、∠C的對邊分別是a、b、c,CD⊥AB于點D,若AC=8,BC=6,求AB、AD、BD的長以及三角形ABC的面積.
在直角三角形ABC中,∠ACB=90°,∠A、∠B、∠C的對邊分別是a、b、c,CD⊥AB于點D,若AC=8,BC=6,求AB、AD、BD的長以及三角形ABC的面積.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
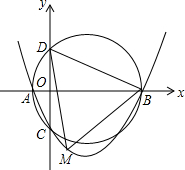 如圖,已知拋物線y=ax2+bx+c(a>0,c<0)交x軸于點A,B,交y軸于點C,設(shè)過點A,B,C的圓與y軸的另一個交點為D.已知點A,B,C的坐標分別為(-2,0),(8,0),(0,-4).
如圖,已知拋物線y=ax2+bx+c(a>0,c<0)交x軸于點A,B,交y軸于點C,設(shè)過點A,B,C的圓與y軸的另一個交點為D.已知點A,B,C的坐標分別為(-2,0),(8,0),(0,-4).查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | 102個 | B. | 104個 | C. | 106個 | D. | 108個 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
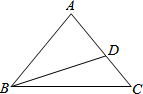 △ABC中,D是AC上一點,AD:DC=2:1,BD=$\sqrt{3}$+1,∠ADB=60°,∠C=45°,試判斷直線AB與△BCD的外接圓是相交還是相切,并證明你的結(jié)論.
△ABC中,D是AC上一點,AD:DC=2:1,BD=$\sqrt{3}$+1,∠ADB=60°,∠C=45°,試判斷直線AB與△BCD的外接圓是相交還是相切,并證明你的結(jié)論.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com