
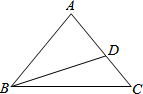
 △ABC中,D是AC上一點,AD:DC=2:1,BD=$\sqrt{3}$+1,∠ADB=60°,∠C=45°,試判斷直線AB與△BCD的外接圓是相交還是相切,并證明你的結論.
△ABC中,D是AC上一點,AD:DC=2:1,BD=$\sqrt{3}$+1,∠ADB=60°,∠C=45°,試判斷直線AB與△BCD的外接圓是相交還是相切,并證明你的結論. 分析 過B作BE⊥AD,E為垂足,不妨設AD=2,CD=1,設ED=x,由∠C=45°,∠ADB=60°,可得到$\sqrt{3}$x=x+1,求出x,利用勾股定理可求出AB=6,因此得到AB2=AD•AC,△ABD∽△ACB,∠ABD=∠ACB=45°,再證明∠ABF=90°,過B作直徑BF即可得到.
解答 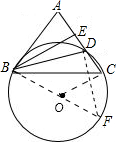 解:直線AB與△BCD的外接圓相切.
解:直線AB與△BCD的外接圓相切.
理由:如圖,⊙O為△BCD的外接圓.過B作BE⊥AD,E為垂足,不妨設AD=2,CD=1,設ED=x,
∵∠C=45°,
∴BE=x+1,
∵∠ADB=60°,
∴BE=$\sqrt{3}$DE=$\sqrt{3}$x,即$\sqrt{3}$x=x+1,
∴x=$\frac{\sqrt{3}+1}{2}$,
則BE=$\frac{3+\sqrt{3}}{2}$,AE=AD-ED=2-x=$\frac{3-\sqrt{3}}{2}$,
在RT△AEB中,AB2=BE2+AE2=($\frac{3+\sqrt{3}}{2}$)2+($\frac{3-\sqrt{3}}{2}$)2=6,
而AD•AC=2×3=6
∴AB2=AD•AC,而∠A公共,
∴△ABD∽△ACB,
∴∠ABD=∠ACB=45°,
過B作直徑BF,則∠ADF=90°,
連DF,則∠F=∠ACB=45°,
∴∠DBF=45°,
∴∠ABF=90°,
∴AB是⊙O的切線,即AB是△BCD的外接圓的切線.
點評 本題考查了直線與圓的位置關系,根據題意作出△BCD的外接圓,構造出直角三角形,利用勾股定理求解是解答此題的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
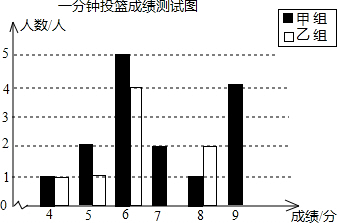
| 成績(分) | 4 | 5 | 6 | 7 | 8 | 9 |
| 甲組(人) | 1 | 2 | 5 | 2 | 1 | 4 |
| 乙組(人) | 1 | 1 | 4 | 5 | 2 | 2 |
| 統計量 | 平均分 | 方差 | 中位數 | 合格率 | 優秀率 |
| 甲組 | 6.8 | 2.56 | 6 | 80.0% | 26.7% |
| 乙組 | 6.8 | 1.76 | 7 | 86.7% | 13.3% |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 941×108 | B. | 94.1×109 | C. | 9.41×1010 | D. | 9.41×1011 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
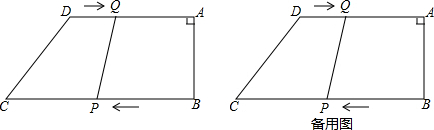
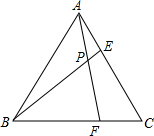 等邊三角形ABC的邊長為6,在AC,BC邊上各取一點E,F,連接AF,BE相交于點P;
等邊三角形ABC的邊長為6,在AC,BC邊上各取一點E,F,連接AF,BE相交于點P;查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | (x+2)2=3 | B. | (x-2)2=4 | C. | (x-2)2=3 | D. | (x-2)2=15 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com