
 已知一次函數y=-$\frac{1}{2}$x+4的圖象與x軸、y軸分別相交于點A、B,四邊形AOBC(O是原點)的一組對邊平行,且AC=5.
已知一次函數y=-$\frac{1}{2}$x+4的圖象與x軸、y軸分別相交于點A、B,四邊形AOBC(O是原點)的一組對邊平行,且AC=5.分析 (1)根據一次函數y=-$\frac{1}{2}$x+4的圖象與x軸、y軸分別相交于點A、B,即可得到點A、B的坐標;
(2)根據梯形的對邊平行,分為AC∥OB,BC∥OA兩種情況,畫出圖形,結合勾股定理求解;
(3)根據C點坐標,一次函數y=kx+b中k<0的條件,確定C的坐標,求一次函數解析式.
解答 解:(1)∵一次函數y=-$\frac{1}{2}$x+4中,當x=0時,y=4;當y=0時,x=8,
∴A(8,0),B(0,4);
(2)∵四邊形AOBC(O是原點)的一組對邊平行,
∴四邊形AOBC是梯形,
在梯形AOBC中,OA=8,OB=4,AC=5,
當AC∥OB時(如圖1),點C的坐標為(8,5),
當BC∥OA時(如圖2),設點C(x,4).
∵AC=5,
∴(x-8)2+(4-0)2=52,
∴x1=5,x2=11,
這時點C的坐標為(5,4)或(11,4),
∴點C的坐標為(8,5)或(5,4)或(11,4);
(3)∵點A、C在一次函數y=kx+b(k<0)的圖象上,
∴點(8,5)與(11,4)都不符合題意,只有當C為(5,4)時,k<0,
∴$\left\{\begin{array}{l}{0=8k+b}\\{4=5k+b}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=\frac{32}{3}}\end{array}\right.$,
∴這個一次函數的解析式為y=-$\frac{4}{3}$x+$\frac{32}{3}$.
點評 本題考查了一次函數的綜合運用,根據組成梯形的字母順序,按照梯形的底邊,需要分類討論求C點坐標,進而得到一次函數解析式.


 新課標快樂提優暑假作業陜西旅游出版社系列答案
新課標快樂提優暑假作業陜西旅游出版社系列答案 暑假銜接培優教材浙江工商大學出版社系列答案
暑假銜接培優教材浙江工商大學出版社系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
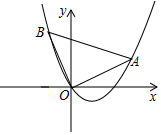 如圖,在平面直角坐標系中,O為坐標原點,△AOB是等腰直角三角形,∠AOB=90°,A(2,1).
如圖,在平面直角坐標系中,O為坐標原點,△AOB是等腰直角三角形,∠AOB=90°,A(2,1).查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{1}{2}$$\sqrt{6}$ | D. | 以上答案都不對 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com