
分析 因為10=9+1,則首先作出以1和3為直角邊的直角三角形,則其斜邊的長即是$\sqrt{10}$.再以原點為圓心,以$\sqrt{10}$為半徑畫弧,和數軸的正半軸交于一點即可;根據6=4+2,2=1+1,分別作出邊長為1的等腰直角三角形,再根據勾股定理即可畫出圖形.
解答 解:∵10=9+1,
∴首先作出以1和3為直角邊的直角三角形,則其斜邊的長即是$\sqrt{10}$.
如圖1,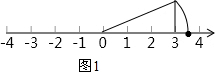 ;
;
∵6=4+2,2=1+1,
∴如圖2,先以點O為圓心,作出邊長為1的等腰直角三角形,以2和AB的長為邊作直角三角形OCD,以點O為圓心,CD為半徑畫弧,與數軸的負半軸交于點E,則E點即為-$\sqrt{6}$所表示的點.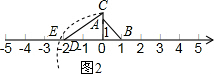 .
.
點評 本題考查勾股定理及實數與數軸的知識,要求能夠正確運用數軸上的點來表示一個無理數,解題關鍵是構造直角三角形,并靈活運用勾股定理.


 新非凡教輔沖刺100分系列答案
新非凡教輔沖刺100分系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
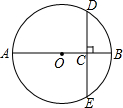 如圖,⊙O的直徑AB=8,弦DE經過OB的中點C且DE⊥OB,則弦DE的長為( )
如圖,⊙O的直徑AB=8,弦DE經過OB的中點C且DE⊥OB,則弦DE的長為( )| A. | 3$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 6$\sqrt{3}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com