
分析 (1)直接利用勾股定理得出c的值即可;
(2)利用a:b=7:25,設a=7x,b=25x,再利用勾股定理得出a的值.
解答 解:(1)∵在△ABC中.∠A,∠B,∠C的對邊分別是a,b,c,∠B=90°,a=9,b=15,
∴c=$\sqrt{{b}^{2}-{a}^{2}}$=$\sqrt{1{5}^{2}-{9}^{2}}$=12;
(2)∵在△ABC中.∠A,∠B,∠C的對邊分別是a,b,c,∠B=90°,a:b=7:25,c=24,
∴設a=7x,b=25x,
則a2+c2=b2,
即(7x)2+242=(25x)2,
解得:x=1,
故a=7.
點評 此題主要考查了勾股定理,根據題意熟練應用勾股定理是解題關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
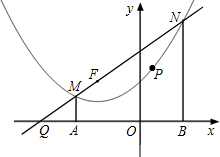 如圖,過點F(-2,2)的直線l與拋物線y=$\frac{1}{4}$x2+x+2交于點M、N兩點(點M在點N的左邊),MA⊥x軸于點A,NB⊥x軸于點B.
如圖,過點F(-2,2)的直線l與拋物線y=$\frac{1}{4}$x2+x+2交于點M、N兩點(點M在點N的左邊),MA⊥x軸于點A,NB⊥x軸于點B.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com