
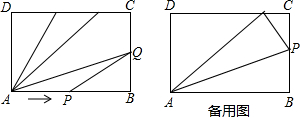
分析 (1)根據題意求出P、Q兩點的速度之比,列出方程,解方程即可;
(2)根據題意分別求出點P到達點D和點Q到達點D所需的時間,計算即可;
(3)分0≤t≤2、2<t≤$\frac{10}{3}$、$\frac{10}{3}$<t≤5三個范圍,根據三角形的面積公式解答即可.
解答 解:(1)∵當點P到達點B時,點Q恰好到達點C,
∴P、Q兩點的速度之比為:6:4=3:2,
設點P的速度是3xcm/s,則點Q的速度是2xcm/s,
由題意得,3x-2x=1,
解得,x=1,
∴點P的速度是3cm/s,則點Q的速度是2cm/s;
(2)點P到達點D所需的時間為:(6+4+6)÷3=$\frac{16}{3}$s,
點Q到達點D所需的時間為:(6+4)÷2=5s,
∴點Q先到達點D,
則點P距離D點16-3×5=1cm,
故答案為:1;
(3)當0≤t≤2時,AP=3t,BQ=2t,
∴△APQ的面積為S=$\frac{1}{2}$×AP×BQ=3t2,
當2<t≤$\frac{10}{3}$時,BP=3t-6,CP=10-3t,CQ=2t-4,QD=10-2t,
∴△APQ的面積為S=6×4-$\frac{1}{2}$×6×(3t-6)-$\frac{1}{2}$×4×(10-2t)-$\frac{1}{2}$×(10-3t)×(2t-4)=3t2-21t+42,
當$\frac{10}{3}$<t≤5時,PQ=6-(3t-10)-[6-(2t-4)]=6-t,
∴△APQ的面積為S=$\frac{1}{2}$×PQ×AD=12-2t.
點評 本題考查的是矩形的性質、等腰三角形的性質,掌握等腰三角形的性質、靈活運用分情況討論思想是解題的關鍵.


 小學教材全測系列答案
小學教材全測系列答案 小學數學口算題卡脫口而出系列答案
小學數學口算題卡脫口而出系列答案 優秀生應用題卡口算天天練系列答案
優秀生應用題卡口算天天練系列答案科目:初中數學 來源: 題型:解答題
 如圖,在△ABC中,∠ABE=2∠C,AD是∠BAC的平分線,BE⊥AD,垂足為E
如圖,在△ABC中,∠ABE=2∠C,AD是∠BAC的平分線,BE⊥AD,垂足為E查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
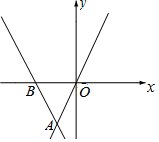 如圖,直線y=kx+b經過點A(-1,m)和點B(-2,0),直線y=2x過點A,則不等式2x<kx+b<0的解集為( )
如圖,直線y=kx+b經過點A(-1,m)和點B(-2,0),直線y=2x過點A,則不等式2x<kx+b<0的解集為( )| A. | x<-2 | B. | -2<x<-1 | C. | -2<x<0 | D. | -1<x<0 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
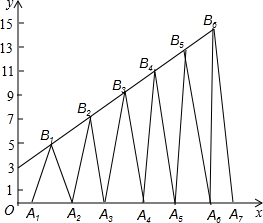 如圖,已知B1(1,y1),B2(2,y2)B3(3,y3)…在直線y=2x+3上,在x軸上取點A1,使OA1=a(0<a<1);作等腰△A1B1A2面積為S1,等腰△A2B2A3面積為S2…;求S2017-S2016=4037-8072a.
如圖,已知B1(1,y1),B2(2,y2)B3(3,y3)…在直線y=2x+3上,在x軸上取點A1,使OA1=a(0<a<1);作等腰△A1B1A2面積為S1,等腰△A2B2A3面積為S2…;求S2017-S2016=4037-8072a.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com