
 如圖,∠AOB=90°,點P為∠AOB內一點.
如圖,∠AOB=90°,點P為∠AOB內一點.分析 (1)過P作BO的垂線,垂足為M,再截取PM=P1M,同方法作P點關于OA的對稱點P1;
(2)根據軸對稱的性質可得BO是P1P2的垂直平分線,AO是P1P的垂直平分線,再根據垂直平分線上的點到線段兩端點距離相等可得P1O=PO,P2O=PO,然后可證明∠1+∠4=90°,再證明∠P1OP2=180°,從而可得P1,O,P2三點在同一直線上;
(3)首先證明四邊形OMPN是矩形,可得∠MPN=90°,再根據直角三角形斜邊上的中線等于斜邊的一半可得OP=$\frac{1}{2}$P1P2,進而可得答案.
解答 (1)解:如圖所示:
(2)證明:
∵P點關于OA、OB的對稱點P1,P2,
∴BO是P2P的垂直平分線,AO是P1P的垂直平分線,
∴P1O=PO,P2O=PO,
∴∠1=∠2,∠3=∠4,
∵∠AOB=90°,
∴∠2+∠3=90°,
∴∠1+∠4=90°,
∴∠P1OP2=180°,
∴P1,O,P2三點在同一直線上;
(3)解:∵P點關于OA、OB的對稱點P1,P2,
∴∠PMO=∠PNO=90°,
∵∠AOB=90°,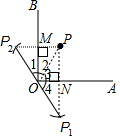
∴四邊形OMPN是矩形,
∴∠MPN=90°,
∵P1O=PO,P2O=PO,
∴P1O=P2O=PO,
∴PO是P1P2的中線,
∴OP=$\frac{1}{2}$P1P2,
∵OP=5,
∴P1P2=10.
點評 此題主要考查了作圖--軸對稱變換,以及直角三角形的性質,關鍵是掌握對稱軸是對稱點連線的垂直平分線.


 名牌學校分層周周測系列答案
名牌學校分層周周測系列答案 黃岡海淀全程培優測試卷系列答案
黃岡海淀全程培優測試卷系列答案科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 已知平面上點A,B,C,D.按下列要求畫出圖形:
已知平面上點A,B,C,D.按下列要求畫出圖形:查看答案和解析>>
科目:初中數學 來源: 題型:填空題
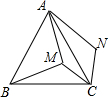 如圖,M為等邊△ABC內部的一點,且MA=8,MB=10,MC=6,將△BMC繞點C順時針旋轉得到△ANC.下列說法中:①MC=NC;②AM=AN;③S四邊形AMCN=S△ABC-S△ABM;④∠AMC=120°.正確的有①③.(請填上番號)
如圖,M為等邊△ABC內部的一點,且MA=8,MB=10,MC=6,將△BMC繞點C順時針旋轉得到△ANC.下列說法中:①MC=NC;②AM=AN;③S四邊形AMCN=S△ABC-S△ABM;④∠AMC=120°.正確的有①③.(請填上番號)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 已知一次函數y1=-x+1,y2=2x-5的圖象如圖所示,根據圖象,解決下列問題:
已知一次函數y1=-x+1,y2=2x-5的圖象如圖所示,根據圖象,解決下列問題:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com