
【題目】已知![]() ,
,![]() 互為相反數,且
互為相反數,且![]() ,
,![]() 、
、![]() 互為倒數,數軸上表示
互為倒數,數軸上表示![]() 的點距原點的距離恰為6個單位長度.
的點距原點的距離恰為6個單位長度.
⑴a= .
⑵求![]() 的值.
的值.
科目:初中數學 來源: 題型:
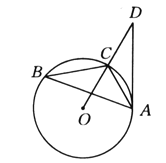
【題目】如圖所示,已知△ABC內接于⊙O,點D在OC的延長線上,sin B=![]() ,∠D=30°.
,∠D=30°.
(1)求證AD是⊙O的切線;
(2)若AC=6,求AD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示的一塊地,已知∠ADC=90°,AD=12m,CD=9m,AB=25m,BC=20m,則這塊地的面積為( )平方米.

A. 96 B. 204 C. 196 D. 304
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為迎接全國文明城市的評選,市政府決定對春風路進行市政化改造,經過市場招標,決定聘請甲、乙兩個工程隊合作施工,已知春風路全長24千米,甲工程隊每天施工的長度比乙工程隊每天施工長度的多施工0.4千米,由甲工程隊單獨施工完成任務所需要的天數是乙工程隊單獨完成任務所需天數的![]() .
.
(1)求甲、乙兩個工程隊每天各施工多少千米?
(2)若甲工程隊每天的施工費用為0.8萬元,乙工程隊每天的施工費用為0.5萬元,要使兩個工程隊施工的總費用不超過7萬元,則甲工程隊至多施工多少天?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】規定:求若干個相同的有理數(均不等于0)的除法運算叫做除方,如2÷2÷2,(-3)÷(-3)÷(-3)÷(-3)等.類比有理數的乘方,我們把2÷2÷2記作2③,讀作“2的圈3次方”,(-3)÷(-3)÷(-3)÷(-3)記作(-3)④,讀作“-3的圈4次方”,一般地,把![]() (a≠0)記作a,讀作“a的圈n次方”.
(a≠0)記作a,讀作“a的圈n次方”.
(初步探究)
(1)直接寫出計算結果:2③=___,(![]() )⑤=___;
)⑤=___;
(2)關于除方,下列說法錯誤的是___
A.任何非零數的圈2次方都等于1;
B.對于任何正整數n,1=1;
C.3④=4③;
D.負數的圈奇數次方結果是負數,負數的圈偶數次方結果是正數.
(深入思考)
我們知道,有理數的減法運算可以轉化為加法運算,除法運算可以轉化為乘法運算,有理數的除方運算如何轉化為乘方運算呢?
(1)試一試:仿照上面的算式,將下列運算結果直接寫成冪的形式.
(-3)④=___;5⑥=___;(-![]() )⑩=___.
)⑩=___.
(2)想一想:將一個非零有理數a的圈n次方寫成冪的形式等于___;
(3)算一算:![]() ÷(
÷(![]() )④×(2)⑤(
)④×(2)⑤(![]() )⑥÷
)⑥÷![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知反比例函數![]() (k為常數,k≠1).
(k為常數,k≠1).
(1)其圖象與正比例函數y=x的圖象的一個交點為P.若點P的縱坐標是2,求k的值;
(2)若在其圖象的每一支上,y隨x的增大而減小,求k的取值范圍;
(3)若其圖象的一支位于第二象限,在這一支上任取兩點A(x1,y1),B(x2,y2),當y1>y2時,試比較x1與x2的大小.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】Rt△ABC中,∠ABC=90°,AB=3,BC=4,過點B的直線把△ABC分割成兩個三角形,使其中只有一個是等腰三角形,則這個等腰三角形的面積是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有依次3個數:2、9、7.對任意相鄰的兩個數,都用右邊的數減去左邊的數,所得之差寫在這兩個數之間,可產生一個新數串:2、7、9、-2、7,這稱為第1次操作,做第2次同樣的操作后也可以產生一個新數串:2、5、7、2、9、-11、-2、9、7,繼續依次操作下去,問從數串2、9、7開始操作第20次后所產生的那個數串的所有數之和是___________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為及時救治新冠肺炎重癥患者,某醫院需購買A、B兩種型號的呼吸機.已知購買一臺A型呼吸機需6萬元,購買一臺B型呼吸機需4萬元,該醫院準備投入資金y萬元,全部用于購進35臺這兩種型號的呼吸機,設購進A型呼吸機x臺.
(1)求y關于x的函數關系式;
(2)若購進B型呼吸機的數量不超過A型呼吸機數量的2倍,則該醫院至少需要投入資金多少萬元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com