
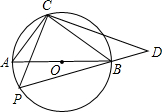
 如圖,⊙O的直徑為6,在⊙O上位于直徑AB的異側(cè)有定點C和動點P.已知BC:CA=4:3,P在半圓上運動,CP⊥CD交PB的延長線于D點.當點P運動到什么位置時,△PCD的面積最大為( )
如圖,⊙O的直徑為6,在⊙O上位于直徑AB的異側(cè)有定點C和動點P.已知BC:CA=4:3,P在半圓上運動,CP⊥CD交PB的延長線于D點.當點P運動到什么位置時,△PCD的面積最大為( )| A. | 36 | B. | 24 | C. | 18 | D. | 12 |
分析 利用圓周角定理得到∠ACB=90°,再利用勾股定理計算出AC=$\frac{18}{5}$,BC=$\frac{24}{5}$,則S△ACB=$\frac{216}{25}$,接著證明Rt△PDC∽Rt△ABC,利用相似三角形的性質(zhì)得到$\frac{{S}_{△PDC}}{{S}_{△ABC}}$=($\frac{PC}{AC}$)2,由于當PC為直徑時最大,S△PDC最大,所以S△PDC的最大值為$\frac{216}{25}$×($\frac{6}{\frac{18}{5}}$)2=24.
解答 解:∵AB為直徑,
∴∠ACB=90°,
在Rt△ACB中,設(shè)BC=4x,AC=3x,
∴AB=5x,
∴5x=6,解得x=$\frac{6}{5}$,
∴AC=$\frac{18}{5}$,BC=$\frac{24}{5}$,
∴S△ACB=$\frac{1}{2}$×$\frac{18}{5}$×$\frac{24}{5}$=$\frac{216}{25}$,
∵∠A=∠P,
∴Rt△PDC∽Rt△ABC,
∴$\frac{{S}_{△PDC}}{{S}_{△ABC}}$=($\frac{PC}{AC}$)2,
∴S△PDC=$\frac{216}{25}$×($\frac{PC}{\frac{18}{5}}$)2,
∴當PC最大時,S△PDC最大,
而PC的最大值為6,
∴S△PDC的最大值為$\frac{216}{25}$×($\frac{6}{\frac{18}{5}}$)2=24.
故選B.
點評 本題考查了三角形相似的判定與性質(zhì):在判定兩個三角形相似時,應(yīng)注意利用圖形中已有的公共角、公共邊等隱含條件,以充分發(fā)揮基本圖形的作用;在利用相似三角形的性質(zhì)時,主要利用相似比計算線段的長.也考查了圓周角定理.


 世紀百通主體課堂小學課時同步達標系列答案
世紀百通主體課堂小學課時同步達標系列答案 世紀百通優(yōu)練測系列答案
世紀百通優(yōu)練測系列答案 百分學生作業(yè)本題練王系列答案
百分學生作業(yè)本題練王系列答案科目:初中數(shù)學 來源: 題型:選擇題
| A. | (-1,3) | B. | (-1,-3) | C. | (3,1) | D. | (1,3) |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
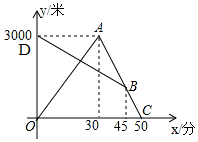 某天早晨,張強從家跑步去體育鍛煉,同時媽媽從體育場晨練結(jié)束回家,途中兩人相遇,張強跑到體育場后發(fā)現(xiàn)要下雨,立即按原路返回,遇到媽媽后兩人一起回到家(張強和媽媽始終在同一條筆直的公路上行走).如圖是兩人離家的距離y(米)與張強出發(fā)的時間x(分)之間的函數(shù)圖象,根據(jù)圖象信息解答下列問題:
某天早晨,張強從家跑步去體育鍛煉,同時媽媽從體育場晨練結(jié)束回家,途中兩人相遇,張強跑到體育場后發(fā)現(xiàn)要下雨,立即按原路返回,遇到媽媽后兩人一起回到家(張強和媽媽始終在同一條筆直的公路上行走).如圖是兩人離家的距離y(米)與張強出發(fā)的時間x(分)之間的函數(shù)圖象,根據(jù)圖象信息解答下列問題:查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
 小明、小華從學校出發(fā)到青少年宮參加書法比賽,小明步行一段時間后,小華騎自行車沿相同路線行進,兩人均勻速前行.他們的路程差s (米)與小明出發(fā)時間t (分)之間的函數(shù)關(guān)系如圖所示.下列說法:
小明、小華從學校出發(fā)到青少年宮參加書法比賽,小明步行一段時間后,小華騎自行車沿相同路線行進,兩人均勻速前行.他們的路程差s (米)與小明出發(fā)時間t (分)之間的函數(shù)關(guān)系如圖所示.下列說法:| A. | ①②④ | B. | ①②③ | C. | ①③④ | D. | ①②③④ |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com