
 如圖,Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,將△ABC繞點C逆時針旋轉至△A′B′C,使得點A′恰好落在AB上,A′B′與BC交于點D,則△A′CD的面積為( )
如圖,Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,將△ABC繞點C逆時針旋轉至△A′B′C,使得點A′恰好落在AB上,A′B′與BC交于點D,則△A′CD的面積為( )| A. | $\frac{\sqrt{3}}{2}$ | B. | 3$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
分析 根據旋轉的性質得CA=CA′=2,∠CA′B′=∠A=60°,則△CAA′為等邊三角形,所以∠ACA′=60°,則可計算出∠BCA′=30°,∠A′DC=90°,然后在Rt△A′DC中利用含30度的直角三角形三邊的關系得A′D=$\frac{1}{2}$CA′=1,CD=$\sqrt{3}$A′D=$\sqrt{3}$,再利用三角形面積公式求解.
解答 解:在Rt△ACB=90°,∵∠B=30°,
∴∠A=60°,
∵△ABC繞點C逆時針旋轉至△A′B′C,使得點A′恰好落在AB上,
∴CA=CA′=2,∠CA′B′=∠A=60°,
∴△CAA′為等邊三角形,
∴∠ACA′=60°,
∴∠BCA′=30°,
∴∠A′DC=90°,
在Rt△A′DC中,∵∠A′CD=30°,
∴A′D=$\frac{1}{2}$CA′=1,CD=$\sqrt{3}$A′D=$\sqrt{3}$,
∴△A′CD的面積=$\frac{1}{2}$×1×$\sqrt{3}$=$\frac{\sqrt{3}}{2}$.
故選A.
點評 本題考查了旋轉的性質:對應點到旋轉中心的距離相等;對應點與旋轉中心所連線段的夾角等于旋轉角;旋轉前、后的圖形全等.也考查了含30度的直角三角形三邊的關系.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:解答題
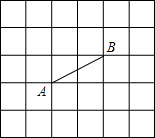 如圖,線段AB是一條格點線段.
如圖,線段AB是一條格點線段.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 有兩個角互余的三角形一定是直角三角形 | |
| B. | 直角三角形中,若一直角邊等于斜邊的一半,則這條直角邊所對的角為30° | |
| C. | 直角三角形斜邊上的中線等于斜邊的一半 | |
| D. | △ABC中,若∠A:∠B:∠C=1:3:5,則這個三角形為直角三角形 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 2.3×10-4 | B. | -2.3×10-4 | C. | -2.3×104 | D. | -2.3×10-5 |
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com