
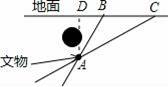
如圖所示,某古代文物被探明埋于地下的A處,由于點A上方有一些管道,考古人員不能垂直向下挖掘,他們被允許從B處或C處挖掘,從B處挖掘時,最短路線BA與地面所成的銳角是56°,從C處挖掘時,最短路線CA與地面所成的銳角是30°,且BC=20m,若考古人員最終從B處挖掘,求挖掘的最短距離.(參考數據:sin56°=0.83,tan56°≈1.48,
 ≈1.73,結果保留整數)
≈1.73,結果保留整數)


【考點】解直角三角形的應用.
【分析】作AD⊥BC交CB延長線于點D,執行額AD即為文物在地面下的深度.設AD=x.通過解直角△ABD求得BD=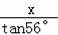
 ;通過解直角△ACD求得CD=
;通過解直角△ACD求得CD=
 x,由此列出關于x的方程,通過方程求得AD的長度.最后通過解直角三角形ABD來求AB的長度即可.
x,由此列出關于x的方程,通過方程求得AD的長度.最后通過解直角三角形ABD來求AB的長度即可.
【解答】解:作AD⊥BC交CB延長線于點D,執行額AD即為文物在地面下的深度.
根據題意得∠CAD=30°,∠ABD=56°.
設AD=x.
在直角△ABD中,∵∠ABD=56°,
∴BD=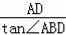
 =
=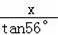
 .
.
在直角△ACD中,∵∠ACB=30°,
∴CD=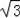
 AD=
AD=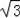
 x,
x,
∴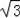
 x=
x=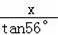
 +20.
+20.
解得x≈18.97,
∴AB=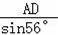
 ≈
≈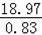
 ≈23.
≈23.
答:從B處挖掘的最短距離為23米.

【點評】此題考查了解直角三角形的應用,主要是正切、余弦概念及運算,關鍵把實際問題轉化為數學問題加以計算.


科目:初中數學 來源: 題型:
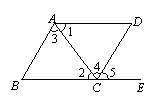
如圖,下列條件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,能判定AB∥CD的條件為 ……………………………………………………………… ( )
A.①②③④ B.①②④ C.①③④ D.①②③
 | |||
 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com