
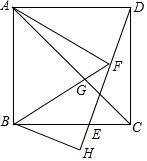
 在正方形ABCD中,點(diǎn)E為BC邊上的一點(diǎn),連接DE,點(diǎn)F為DE的中點(diǎn),連接FA、FB,線段FB與AC交于點(diǎn)G,過B作BH⊥DE交DE的延長線于點(diǎn)H,若BH=3,AG:GC=$\sqrt{3}$:1,則△AFG的面積為9$\sqrt{3}$-$\frac{27}{2}$.
在正方形ABCD中,點(diǎn)E為BC邊上的一點(diǎn),連接DE,點(diǎn)F為DE的中點(diǎn),連接FA、FB,線段FB與AC交于點(diǎn)G,過B作BH⊥DE交DE的延長線于點(diǎn)H,若BH=3,AG:GC=$\sqrt{3}$:1,則△AFG的面積為9$\sqrt{3}$-$\frac{27}{2}$. 分析 根據(jù)正方形的性質(zhì)求得AD=BC,∠BCD=90°,然后根據(jù)直角三角形斜邊上中線的性質(zhì)求得CG=GE=GD,∠GCD=∠GDC,根據(jù)等量減等量求得∠BCG=∠ADG,根據(jù)SAS求得△ADG≌△BCG,從而證得GA=GB,過點(diǎn)H作HN⊥BC于N,根據(jù)正方形的性質(zhì)可得△CHN為等腰直角三角形,根據(jù)等腰直角三角形的性質(zhì)可得HN=CN,再根據(jù)平行線分線段成比例定理求出$\frac{BN}{CN}$=$\sqrt{3}$,即$\frac{HN}{BN}$=$\sqrt{3}$,然后求出∠HBN=30°,然后判斷出△ABG是等邊三角形,再求出∠AGD=75°,然后根據(jù)平角等于180°求出∠BGM=45°,再根據(jù)等腰直角三角形的斜邊等于直角邊的$\sqrt{2}$得到AB=AF=BF=3$\sqrt{2}$,根據(jù)三角形的面積公式即可得到結(jié)論.
解答 解:連接CF,
∵四邊形ABCD是正方形,
∴AD=BC,∠BCD=90°,
又∵點(diǎn)F為DE中點(diǎn),
∴CF=FE=FD,
∴∠FCD=∠FDC,
∴∠BCF=∠ADF,
在△ADF與△BCF中,
$\left\{\begin{array}{l}{AD=BC}\\{∠ADF=∠BCF}\\{DF=CF}\end{array}\right.$,
∴△ADF≌△BCF(SAS),
∴FA=FB,
如圖,過點(diǎn)G作GN⊥BC于N,
∵AC是正方形ABCD的對角線,
∴∠ACB=45°,
∴△CGN為等腰直角三角形,
∴GN=CN,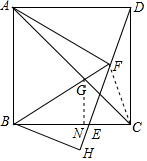
易得AB∥GN,
∴$\frac{BN}{CN}$=$\frac{AG}{CG}$=$\sqrt{3}$,
∴$\frac{BN}{GN}$=$\sqrt{3}$,
∴∠GBN=30°,
∵∠ABC=90°,
∴∠ABG=90°-30°=60°,
由(1)知FA=FB,
∴△ABF是等邊三角形,
∴AD=AF=AB,
∴∠AFD=$\frac{1}{2}$(180°-30°)=75°,
∴∠BFH=180°-75°-60°=45°,
∵BH⊥DE,
∴△BHF是等腰直角三角形,
∴BF=$\sqrt{2}$BH=3$\sqrt{2}$,
∴AF=AB=3$\sqrt{2}$,
∴AC=6,
∴AG=9-3$\sqrt{3}$,
∴$\frac{{S}_{△ABG}}{{S}_{△ABC}}$=$\frac{9-3\sqrt{3}}{6}$,
∵S△ABC=9,
∴S△ABG=$\frac{27-9\sqrt{3}}{2}$,
∵S△ABF=$\frac{\sqrt{3}}{4}$×(3$\sqrt{2}$)2=$\frac{9\sqrt{3}}{2}$,
∴△AFG的面積=S△ABF-S△ABG=9$\sqrt{3}$-$\frac{27}{2}$.
故答案為:9$\sqrt{3}$-$\frac{27}{2}$.
點(diǎn)評 本題考查了正方形的性質(zhì),全等三角形的判定與性質(zhì),等腰直角三角形的判定與性質(zhì),等邊三角形的判定與性質(zhì),難點(diǎn)在于(2)作輔助線構(gòu)造出等腰直角三角形和含30°角的直角三角形,求出∠HBN=30°是本題的難點(diǎn),也是關(guān)鍵.


 點(diǎn)睛新教材全能解讀系列答案
點(diǎn)睛新教材全能解讀系列答案 小學(xué)教材完全解讀系列答案
小學(xué)教材完全解讀系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 0.28×106 | B. | 2.8×105 | C. | 28×104 | D. | 280×103 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | -$\frac{1}{3}$ab2c和cab2 | B. | xy2和x2y | C. | -$\frac{1}{2}$和0 | D. | $\frac{xy}{3}$和-xy |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
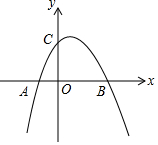 如圖,二次函數(shù)y=-x2+2x+k的圖象經(jīng)過點(diǎn)C(0,6),與x軸交于A,B兩點(diǎn)
如圖,二次函數(shù)y=-x2+2x+k的圖象經(jīng)過點(diǎn)C(0,6),與x軸交于A,B兩點(diǎn)查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
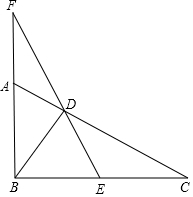 如圖,在Rt△ABC中,∠ABC=90°,BD⊥AC于D,E是BC中點(diǎn),ED的延長線交BA的延長線于F,求證:AB:BC=DF:BF.
如圖,在Rt△ABC中,∠ABC=90°,BD⊥AC于D,E是BC中點(diǎn),ED的延長線交BA的延長線于F,求證:AB:BC=DF:BF.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 14x2-2y | B. | 2x2-2y | C. | 2x2-6y | D. | 14x2-6y |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | ②③⑤ | B. | ②④ | C. | ①③ | D. | ① |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com