
分析 (1)先根據(jù)點(diǎn)E,F(xiàn)的坐標(biāo)確定出圖形的位置,然后分0<a<2和a>2兩種情況,根據(jù)三角形的外角的性質(zhì)得出∠AOF=∠EBO,進(jìn)而得出結(jié)論;
(2)先根據(jù)點(diǎn)E,F(xiàn),A,B的坐標(biāo)確定出BE=$\sqrt{2}$a和AF=$\sqrt{2}$b,再利用(1)得出的相似得出比例式即可找出ab=2;
(3)分兩種情況利用三角形的面積的和差即可得出結(jié)論.
解答 解:(1)△AOF∽△BEO;
理由:∵點(diǎn)E在直線y=-x+2上,且點(diǎn)E的橫坐標(biāo)是a,
∴E(a,-a+2),
∵點(diǎn)F在直線y=-x+2上,且點(diǎn)F的縱坐標(biāo)是b,
∴F(2-b,b),∵a>0,b>0,
當(dāng)-a+2>0,時(shí),即:0<a<2時(shí),
如圖1,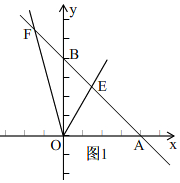 ∵一次函數(shù)y=-x+2與x軸交于點(diǎn)A,與y軸交于點(diǎn)B,
∵一次函數(shù)y=-x+2與x軸交于點(diǎn)A,與y軸交于點(diǎn)B,
∴A(2,0),B(0,2),
∴OA=OB,
∴∠OAB=∠OBA=45°,
∴∠BEO=∠OAB+∠AOE=45°+∠AOE,
∵∠EOF=45°,
∴∠AOF=∠EOF+∠AOE=∠45°+∠AOE,
∴∠AOF=∠AEO,
∵∠OAF=∠EBO=45°,
∴△AOF∽△BEO;
當(dāng)-a+2<0時(shí),即:a>2時(shí),
如圖2,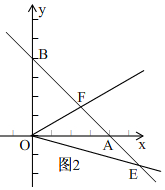 ∵一次函數(shù)y=-x+2與x軸交于點(diǎn)A,與y軸交于點(diǎn)B,
∵一次函數(shù)y=-x+2與x軸交于點(diǎn)A,與y軸交于點(diǎn)B,
∴A(2,0),B(0,2),
∴OA=OB,
∴∠OAB=∠OBA=45°,
∴∠BEO=∠OAB-∠AOE=45°-∠AOE,
∵∠EOF=45°,
∴∠AOF=∠EOF-∠AOE=∠45°-∠AOE,
∴∠AOF=∠AEO,
∵∠OAF=∠EBO=45°,
∴△AOF∽△BEO;
(2)ab=2;
理由:∵點(diǎn)E在直線y=-x+2上,且點(diǎn)E的橫坐標(biāo)是a,
∴E(a,-a+2),
∵B(0,2),
∴BE=$\sqrt{{a}^{2}+(-a+2-2)^{2}}$=$\sqrt{2}$a
∵點(diǎn)F在直線y=-x+2上,且點(diǎn)F的縱坐標(biāo)是b,
∴F(2-b,b),
∵A(2,0),
∴AF=$\sqrt{(2-b-2)^{2}+{b}^{2}}$=$\sqrt{2}$b,
由(1)知,OA=OB=2,△AOF∽△BEO,
∴$\frac{OA}{BE}=\frac{AF}{OB}$,
∴$\frac{2}{\sqrt{2}a}=\frac{\sqrt{2}b}{2}$,
∴ab=2;
(3)當(dāng)0<a<2時(shí),由(1)知,OA=OB=2,
∴S△OEF=S△AOF-S△AOE=$\frac{1}{2}$OA•|yF|-$\frac{1}{2}$OA•|yE|=$\frac{1}{2}$OA(|yF|-|yE|=$\frac{1}{2}$×2[b-(-a+2)]=a+b-2;
當(dāng)a>2時(shí),由(1)知,OA=OB=2,
∴S△OEF=S△AOF+S△AOE=$\frac{1}{2}$OA•|yF|+$\frac{1}{2}$OA•|yE|=$\frac{1}{2}$OA(|yF|+|yE|=$\frac{1}{2}$×2[b+(a-2)]=a+b-2;
即:△OEF的面積為a+b-2.
點(diǎn)評(píng) 此題是相似三角形的綜合題,主要考查了三角形的外角,相似三角形的判定和性質(zhì),三角形的面積公式,解答(1)的關(guān)鍵是利用三角形的外角的性質(zhì)得出∠AOF=∠EBO,解答(2)的關(guān)鍵是求出AF=$\sqrt{2}$b,BE=$\sqrt{2}$a;畫(huà)出圖形是解本題的難點(diǎn).



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | $\frac{7}{25}$ | B. | $\frac{7}{32}$ | C. | $\frac{3}{80}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
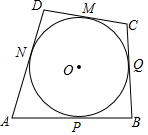 己知四邊形ABCD的邊AB、BC、CD、DA分別與⊙O相切于P、Q、M、N,探究四邊形四邊有何特點(diǎn).
己知四邊形ABCD的邊AB、BC、CD、DA分別與⊙O相切于P、Q、M、N,探究四邊形四邊有何特點(diǎn).查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 6 | B. | 9 | C. | $\frac{9}{2}$ | D. | $\frac{81}{4}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
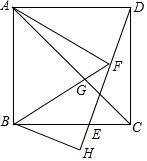 在正方形ABCD中,點(diǎn)E為BC邊上的一點(diǎn),連接DE,點(diǎn)F為DE的中點(diǎn),連接FA、FB,線段FB與AC交于點(diǎn)G,過(guò)B作BH⊥DE交DE的延長(zhǎng)線于點(diǎn)H,若BH=3,AG:GC=$\sqrt{3}$:1,則△AFG的面積為9$\sqrt{3}$-$\frac{27}{2}$.
在正方形ABCD中,點(diǎn)E為BC邊上的一點(diǎn),連接DE,點(diǎn)F為DE的中點(diǎn),連接FA、FB,線段FB與AC交于點(diǎn)G,過(guò)B作BH⊥DE交DE的延長(zhǎng)線于點(diǎn)H,若BH=3,AG:GC=$\sqrt{3}$:1,則△AFG的面積為9$\sqrt{3}$-$\frac{27}{2}$.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 36.1×107 | B. | 3.61×107 | C. | 3.61×108 | D. | 3.61×109 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 10 | B. | 2 | C. | 1 | D. | 5 |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com