
分析 (1)根據待定系數法,可得函數解析式;
(2)根據函數值相等的兩點關于對稱軸對稱,可得A、C關于對稱軸對稱,根據兩點之間線段最短,可得AB,根據勾股定理,可得AB的長,根據自變量與函數值的對應關系,可得M的坐標;
(3)當AB⊥AP時,點P到直線AB的距離最大.
解答  解:(1)將A、B、C的坐標代入函數解析式,得$\left\{\begin{array}{l}{9a-3b+c=0}\\{c=3}\\{a+b+c=0}\end{array}\right.$,
解:(1)將A、B、C的坐標代入函數解析式,得$\left\{\begin{array}{l}{9a-3b+c=0}\\{c=3}\\{a+b+c=0}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{a=-1}\\{b=-2}\\{c=3}\end{array}\right.$,
拋物線的解析式為y=-x2-2x+3;
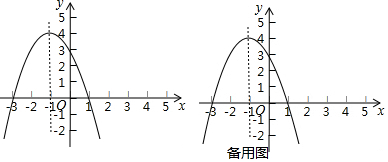
(2)如圖1,連接AB交對稱軸于M,連接MC,
由A、C關于對稱軸對稱,得AM=MC.
由兩點間線段最短,得
MB+MC=AM+MB=AB.
由勾股定理,得AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=3$\sqrt{2}$,
即MB+MC=3$\sqrt{2}$,
設AB的解析式為y=kx+t(k≠0),將A、B坐標代入,得
$\left\{\begin{array}{l}{-3k+t=0}\\{t=3}\end{array}\right.$
解得$\left\{\begin{array}{l}{k=1}\\{t=3}\end{array}\right.$,
則直線AB的解析式為y=x+3,
當x=-1時,y=2,即M(-1,2);
(3)如圖2,當AB⊥AP時,點P到直線AB的距離最大.
設AP交y軸于點Q.
∵OA=OB,∠AOB=90°,
∴∠BAO=∠ABO=45°,
∴∠OBP=45°,
∴OA=OQ=3,
易得直線AQ的解析式為:y=-x-3,
則$\left\{\begin{array}{l}{y=-x-3}\\{y=-{x}^{2}-2x+3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=2}\\{y=-5}\end{array}\right.$或$\left\{\begin{array}{l}{x=-3}\\{y=0}\end{array}\right.$(舍去),
此時P(2,-5).
則PA=$\sqrt{[2-(-3)]^{2}+(-5-0)^{2}}$=5$\sqrt{2}$.
即點P到直線AB的最大距離是5$\sqrt{2}$.
點評 本題考查了二次函數綜合題,利用待定系數法求函數解析式;利用兩點之間線段最短得出AB=BM+CM是解題關鍵;利用圖形得到“當AB⊥AP時,點P到直線AB的距離最大”是解題的關鍵.


 字詞句段篇系列答案
字詞句段篇系列答案科目:初中數學 來源: 題型:解答題
 如圖,△ABC中,CD是邊AB上的高,且$\frac{AD}{CD}$=$\frac{CD}{BD}$.
如圖,△ABC中,CD是邊AB上的高,且$\frac{AD}{CD}$=$\frac{CD}{BD}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
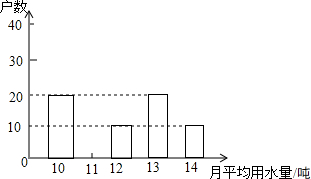 為了倡導“節約用水,從我做起”,某市政府決定對市直機關600戶家庭的用水情況作一次調查,市政府調查小組隨機抽查了其中的100戶家庭一年的月平均用水量 (單位:噸),并將調查結果制成了如圖所示的條形統計圖.
為了倡導“節約用水,從我做起”,某市政府決定對市直機關600戶家庭的用水情況作一次調查,市政府調查小組隨機抽查了其中的100戶家庭一年的月平均用水量 (單位:噸),并將調查結果制成了如圖所示的條形統計圖.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖所示,P是等邊△ABC內的一點,連結PA、PB、PC,將△BAP繞B點順時針旋轉60°得△BCQ,連結PQ,若PA2+PB2=PC2,則∠APB等于( )
如圖所示,P是等邊△ABC內的一點,連結PA、PB、PC,將△BAP繞B點順時針旋轉60°得△BCQ,連結PQ,若PA2+PB2=PC2,則∠APB等于( )| A. | 150° | B. | 145° | C. | 140° | D. | 135° |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com