
如圖,∠BAC=∠DAF=90°,AB=AC,AD=AF,點D、E為BC邊上的兩點,且∠DAE=45°,連接EF、BF,則下列結論:
①△AED≌△AEF
②△AED為等腰三角形
③BE+DC>DE
④BE2+DC2=DE2 ,
其中正確結論的個數是( )

A.1 B.2 C.3 D.4
C
【解析】
試題分析::①∵∠DAF=90°,∠DAE=45°,∴∠FAE=∠DAF-∠DAE=45°.在△AED與△AEF中,AD=AF,∠DAE=∠FAE=45°,AE=AE,∴△AED≌△AEF(SAS),①正確;②∵∠BAC=90°,AB=AC,∴∠ABE=∠C=45°.∵點D、E為BC邊上的兩點,∠DAE=45°,∴AD與AE不一定相等,②錯誤;③∵∠BAC=∠DAF=90°,∴∠BAC-∠BAD=∠DAF-∠BAD,即∠CAD=∠BAF.在△ACD與△ABF中,AC=AB,∠CAD=∠BAF,AD=AF,∴△ACD≌△ABF(SAS),∴CD=BF,由①知△AED≌△AEF,∴DE=EF.在△BEF中,∵BE+BF>EF,∴BE+DC>DE,③正確;④由③知△ACD≌△ABF,∴∠C=∠ABF=45°,∵∠ABE=45°,∴∠EBF=∠ABE+∠ABF=90°.在Rt△BEF中,由勾股定理,得 ,∵BF=DC,EF=DE,∴
,∵BF=DC,EF=DE,∴ ,④正確.所以正確的結論有①③④.故選C.
,④正確.所以正確的結論有①③④.故選C.
考點:1.等腰直角直角三角形的性質;2.全等三角形的判定與性質;3.勾股定理.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源:2014-2015學年浙江省余姚市九年級上學期第一次質量分析數學試卷(解析版) 題型:選擇題
若二次函數y=ax2+bx+c,當x取x1,x2(x1≠x2)時,函數值相等,則當x取x1+x2時,函數值為( )
(A)a+c (B)a-c (C)-c (D)c
查看答案和解析>>
科目:初中數學 來源:2014-2015學年浙江省余姚市九年級上學期第一次質量分析數學試卷(解析版) 題型:填空題
二次函數y=x2+2x+k的圖象上有四個點A(2,y1)、B(2+a,y2)、C(a-1,y3)、D(m,y4),若AB‖CD,則m= .
查看答案和解析>>
科目:初中數學 來源:2014-2015學年浙江省嘉興市實驗學校九年級上學期期中考試數學試卷(解析版) 題型:解答題
在一個不透明的布袋里裝有4個標號為1、2、3、4的小球,它們的材質、形狀、大小完全相同,小凱從布袋里隨機取出一個小球,記下數字為x,小敏從剩下的3個小球中隨機取出一個小球,記下數字為y,這樣確定了點P的坐標(x,y).
(1)請你運用畫樹狀圖或列表的方法,寫出點P所有可能的坐標;
(2)求點(x,y)在函數 圖象上的概率.
圖象上的概率.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年浙江省嘉興市實驗學校九年級上學期期中考試數學試卷(解析版) 題型:解答題
如圖1,已知拋物線y=-x2+bx+c經過點A(1,0),B(-3,0)兩點,且與y軸交于點C.

(1)求b,c的值。
(2)在第二象限的拋物線上,是否存在一點P,使得△PBC的面積最大?求出點P的坐標及△PBC的面積最大值.若不存在,請說明理由.
(3)如圖2,點E為線段BC上一個動點(不與B,C重合),經過B、E、O三點的圓與過點B且垂直于BC的直線交于點F,當△OEF面積取得最小值時,求點E坐標.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年浙江省嘉興市八年級上學期期中考試數學試卷(解析版) 題型:解答題
(10分)(1)如圖(1),已知:在△ABC中,∠BAC=90°,AB=AC,直線m經過點A,BD⊥直線m, CE⊥直線m,垂足分別為點D、E.證明:DE=BD+CE.
(2)如圖(2),將(1)中的條件改為:在△ABC中,AB=AC,D、A、E三點都在直線m上,并且有∠BDA=∠AEC=∠BAC= ,其中
,其中 為任意銳角或鈍角.請問結論DE=BD+CE是否成立?如成立,請你給出證明;不成立,請說明理由.
為任意銳角或鈍角.請問結論DE=BD+CE是否成立?如成立,請你給出證明;不成立,請說明理由.
(3)拓展與應用:如圖(3),D、E是D、A、E三點所在直線m上的兩動點(D、A、E三點互不重合),點F為∠BAC平分線上的一點,且△ABF和△ACF均為等邊三角形,連接BD、CE,若∠BDA=∠AEC=∠BAC,試判斷△DEF的形狀,并給出證明.

查看答案和解析>>
科目:初中數學 來源:2014-2015學年浙江省寧波市九年級10月月考數學試卷(解析版) 題型:選擇題
當 時,下列函數:①
時,下列函數:① ;②
;② ;③
;③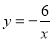 ;④
;④ ,函數值
,函數值 隨自變量
隨自變量 增大而增大的有( )
增大而增大的有( )
A.①② B.①②③ C.①②④ D.①②③④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com