
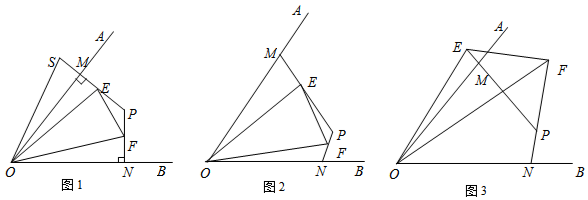
分析 (1)結論:相等,EF=FN+EM.先證明△OMS≌△ONF,再證明△OES≌△OEF即可解決問題.
(2)結論:EF=FN+EM.如圖2中,延長EM到S,使得SM=FN,連接SO,先證明△OMS≌△ONF,再證明△OES≌△OEF即可解決問題.
(3)結論:EF=FN-EM.如圖3中,延長ME到S,使得MS=FN,連接SO,先證明△OMS≌△ONF,再證明△OES≌△OEF即可解決問題.
解答 解:(1)結論:相等,EF=FN+EM.
理由:如圖1中,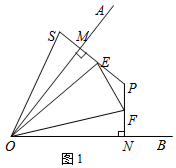
在△OMS和△ONF中,
$\left\{\begin{array}{l}{OM=ON}\\{∠OMS=∠ONF}\\{MS=FN}\end{array}\right.$,
∴△OMS≌△ONF,
∴OS=OF,∠SOM=∠FON,
∵∠EOF=$\frac{1}{2}$∠MON=∠EOM+∠FON=∠EOM+∠SOM=∠SOE,
在△OES和△OEF中,
$\left\{\begin{array}{l}{OE=OE}\\{∠SOE=∠EOF}\\{OS=OF}\end{array}\right.$,
∴△OES≌△OEF,
∴EF=SE=SM+EM=FN+EM.
故答案為相等,EF=FN+EM.
(2)如圖2中,延長EM到S,使得SM=FN,連接SO.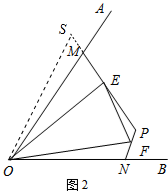
∵∠OMP+∠ONP=180°,∠OMS+∠OMP=180°,
∴∠OMS=∠ONF,
在△OMS和△ONF中,
$\left\{\begin{array}{l}{OM=ON}\\{∠OMS=∠ONF}\\{MS=FN}\end{array}\right.$,
∴△OMS≌△ONF,
∴OS=OF,∠SOM=∠FON,
∵∠EOF=$\frac{1}{2}$∠MON=∠EOM+∠FON=∠EOM+∠SOM=∠SOE,
在△OES和△OEF中,
$\left\{\begin{array}{l}{OE=OE}\\{∠SOE=∠EOF}\\{OS=OF}\end{array}\right.$,
∴△OES≌△OEF,
∴EF=SE=SM+EM=FN+EM.
(3)結論:EF=FN-EM.
理由:如圖3中,延長ME到S,使得MS=FN,連接SO.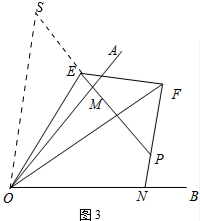
∵∠OMP+∠ONP=180°,∠OMS+∠OMP=180°,
∴∠OMS=∠ONF,
在△OMS和△ONF中,
$\left\{\begin{array}{l}{OM=ON}\\{∠OMS=∠ONF}\\{MS=FN}\end{array}\right.$,
∴△OMS≌△ONF,
∴OS=OF,∠SOM=∠FON,
∵∠EOF=$\frac{1}{2}$∠MON=∠EOM+∠FON=∠EOM+∠SOM=∠SOE,
在△OES和△OEF中,
$\left\{\begin{array}{l}{OE=OE}\\{∠SOE=∠EOF}\\{OS=OF}\end{array}\right.$,
∴△OES≌△OEF,
∴EF=SE=SM-EM=FN-EM.
點評 本題考查三角形綜合題、全等三角形的判定和性質等知識,解題的關鍵是熟練掌握全等三角形的判定和性質,學會添加常用輔助線,構造全等三角形,屬于中考常考題型.


科目:初中數學 來源: 題型:選擇題
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 0.215×104 | B. | 2.15×103 | C. | 2.15×104 | D. | 21.5×102 |
查看答案和解析>>
科目:初中數學 來源:2016-2017學年四川省成都市金堂縣八年級上學期期末考試數學試卷就(解析版) 題型:填空題
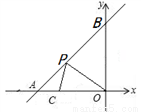
如圖,直線y=x+6與x軸、y軸分別交于點A和點B,x軸上有一點C(﹣4,0),點P為直線一動點,當PC+PO值最小時點P的坐標為_______
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
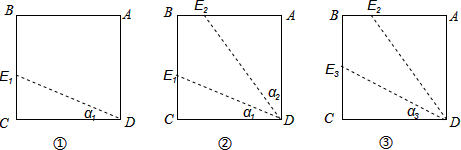
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com