
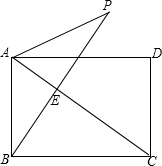
 如圖,矩形ABCD中,AB=6,BC=8,過點B作BE⊥AC,垂足為E,把△ABE沿AE翻折,得△APE.
如圖,矩形ABCD中,AB=6,BC=8,過點B作BE⊥AC,垂足為E,把△ABE沿AE翻折,得△APE.分析 (1)先根據勾股定理求得AB=10,再由S△ABC=$\frac{1}{2}$AC•BE=$\frac{1}{2}$AB•BC可得PE=BE的值;
(2)分三種情況:①0<x≤$\frac{14}{5}$時,利用勾股定理求得A′E′=AE=$\frac{18}{5}$、AE′=x+$\frac{18}{5}$、ME′=AE′tan∠CAD=$\frac{3}{4}$(x+$\frac{18}{5}$),證△AJN∽△ADC、△A′JN∽△A′P′E′得$\frac{AJ}{NJ}$=$\frac{AD}{CD}$、$\frac{A′J}{A′E′}$=$\frac{NJ}{P′E′}$,設A′J=m、NJ=n,可由$\frac{x+m}{n}=\frac{8}{6}$、$\frac{m}{\frac{18}{5}}$=$\frac{m}{\frac{24}{5}}$得NJ=$\frac{12}{7}$x,根據S重疊=S△AE′M-S△AA′N可得;
②$\frac{14}{5}$<x≤$\frac{32}{5}$時,由AC=10、AA′=x知A′C=10-x,過點M作MK⊥A′C,由∠1=∠2=∠3=∠4知MA′=MC=10-x,從而得CK=$\frac{1}{2}$A′C=$\frac{10-x}{2}$、MK=CKtan∠4=$\frac{2}{3}$(10-x),由CE′=CE-EE′=$\frac{32}{5}$-x得NE′=CE′tan∠4=$\frac{4}{3}$($\frac{32}{5}$-x),根據S重疊=S△A′CM-S△CE′N可得;
③$\frac{32}{5}$<x≤10時,A′C=AC-AA′,過點M作MK⊥A′C于點K,由②知MA′=MC即可得CK=$\frac{1}{2}$A′C=$\frac{1}{2}$(10-x),從而有MK=CMtan∠MCK=$\frac{2}{3}$(10-x),根據S重疊=$\frac{1}{2}$A′C•MK可得答案.
解答 解:(1)∵AB=6、BC=8,
∴AB=$\sqrt{A{B}^{2}+B{C}^{2}}$=10,
∵BE⊥AC,
∴S△ABC=$\frac{1}{2}$AC•BE=$\frac{1}{2}$AB•BC,即$\frac{1}{2}$×10×BE=$\frac{1}{2}$×6×8,
解得:BE=$\frac{24}{5}$,
∵△ABE沿AE翻折得△APE,
∴PE=BE=$\frac{24}{5}$;
(2)①如圖1,當0<x≤$\frac{14}{5}$時,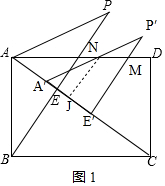
∵AP=AB=6、PE=BE=$\frac{24}{5}$,
∴A′E′=AE=$\sqrt{A{P}^{2}-A{E}^{2}}$=$\sqrt{{6}^{2}-(\frac{24}{5})^{2}}$=$\frac{18}{5}$,
則AE′=x+$\frac{18}{5}$,
∴ME′=AE′tan∠CAD=AE′×$\frac{CD}{AD}$=$\frac{6}{8}$(x+$\frac{18}{5}$)=$\frac{3}{4}$(x+$\frac{18}{5}$),
過點N作NJ⊥AC于點J,則∠NJA=∠CDA=∠P′E′A′,
∵∠JAN=∠DAC、∠JA′N=∠E′A′P′,
∴△AJN∽△ADC、△A′JN∽△A′P′E′,
∴$\frac{AJ}{NJ}$=$\frac{AD}{CD}$、$\frac{A′J}{A′E′}$=$\frac{NJ}{P′E′}$,
設A′J=m,NJ=n,
∴$\frac{x+m}{n}=\frac{8}{6}$、$\frac{m}{\frac{18}{5}}$=$\frac{m}{\frac{24}{5}}$,
解得:n=$\frac{12}{7}$x,即NJ=$\frac{12}{7}$x,
∴S重疊=S△AE′M-S△AA′N=$\frac{1}{2}$(x+$\frac{18}{5}$)•$\frac{3}{4}$(x+$\frac{18}{5}$)-$\frac{1}{2}$•x•$\frac{12}{7}$x=-$\frac{27}{56}$x2+$\frac{27}{10}$x+$\frac{241}{50}$;
②如圖2,當$\frac{14}{5}$<x≤$\frac{32}{5}$時,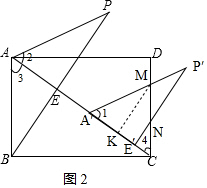
∵AC=10、AA′=x,
則A′C=10-x,
過點M作MK⊥A′C,
∵∠1=∠2=∠3=∠4,
∴MA′=MC=10-x,
則CK=$\frac{1}{2}$A′C=$\frac{10-x}{2}$,
∴MK=CKtan∠4=CK•$\frac{AD}{CD}$=$\frac{10-x}{2}$×$\frac{8}{6}$=$\frac{2}{3}$(10-x),
∵CE′=CE-EE′=CA-AE-EE′=10-$\frac{18}{5}$-x=$\frac{32}{5}$-x,
∴NE′=CE′tan∠4=CE′•$\frac{AD}{CD}$=($\frac{32}{5}$-x)×$\frac{8}{6}$=$\frac{4}{3}$($\frac{32}{5}$-x),
∴S重疊=S△A′CM-S△CE′N=$\frac{1}{2}$×(10-x)•$\frac{2}{3}$(10-x)-$\frac{1}{2}$×($\frac{32}{5}$-x)•$\frac{4}{3}$($\frac{32}{5}$-x)=-$\frac{1}{3}$x2+$\frac{28}{15}$x+$\frac{452}{75}$;
③如圖3,當$\frac{32}{5}$<x≤10時,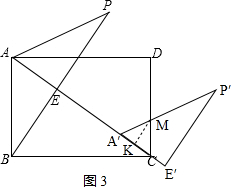
∵A′C=AC-AA′,
∴過點M作MK⊥A′C于點K,
由②知MA′=MC,
∴CK=$\frac{1}{2}$A′C=$\frac{1}{2}$(10-x),
則MK=CMtan∠MCK=CM•$\frac{AD}{CD}$=$\frac{1}{2}$(10-x)•$\frac{8}{6}$=$\frac{2}{3}$(10-x),
∴S重疊=$\frac{1}{2}$A′C•MK=$\frac{1}{2}$(10-x)•$\frac{2}{3}$(10-x)=$\frac{1}{3}$x2-$\frac{20}{3}$x+$\frac{100}{3}$;
綜上,y=$\left\{\begin{array}{l}{-\frac{27}{56}{x}^{2}+\frac{27}{10}x+\frac{241}{50}}&{(0<x≤\frac{14}{5})}\\{-\frac{1}{3}{x}^{2}+\frac{28}{15}x+\frac{452}{75}}&{(\frac{14}{5}<x≤\frac{32}{5})}\\{\frac{1}{3}{x}^{2}-\frac{20}{3}x+\frac{100}{3}}&{(\frac{32}{5}<x≤10)}\end{array}\right.$.
點評 本題主要考查四邊形的綜合,考查的知識點有翻折的性質、平移的性質、勾股定理、解直角三角形、相似三角形的判定與性質及等腰三角形的判定與性質等,根據割補法求三角形面積利用解直角三角形、相似三角形的判定與性質及等腰三角形的判定與性質得出所需線段的長度是解題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
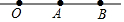 如圖,O,A,B三點在同一直線上,則下列說法中正確的是( )
如圖,O,A,B三點在同一直線上,則下列說法中正確的是( )| A. | 射線OA與射線AO表示同一條射線 | B. | 射線OA大于射線AB | ||
| C. | 射線OA與射線OB表示同一條射線 | D. | 線段OA與線段AO表示兩條不同線段 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
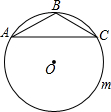 如圖,△ABC中,AB=BC,∠ABC=120°,AC=2$\sqrt{3}$,⊙O是△ABC的外接圓,D是優弧AmC上任意一點(不包括A,C),記四邊形ABCD的周長為y,BD的長為x,則y關于x的函數關系式是( )
如圖,△ABC中,AB=BC,∠ABC=120°,AC=2$\sqrt{3}$,⊙O是△ABC的外接圓,D是優弧AmC上任意一點(不包括A,C),記四邊形ABCD的周長為y,BD的長為x,則y關于x的函數關系式是( )| A. | y=$\frac{\sqrt{3}}{4}$x+4 | B. | y=$\sqrt{3}$x+4 | C. | y=$\sqrt{3}$x2+4 | D. | y=$\frac{\sqrt{3}}{4}$x2+4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com