
分析 把方程②因式分解為兩個二元一次方程,分別和①組成新的方程組,分別求出兩個二元一次方程組的解.
解答 解:$\left\{\begin{array}{l}{x+y=5①}\\{{x}^{2}-3xy+2{y}^{2}=0②}\end{array}\right.$
由②,得(x-2y)(x-y)=0,
即x-2y=0③,或x-y=0④
由①③、①④分別組成方程組,得
$\left\{\begin{array}{l}{x+y=5}\\{x-2y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x+y=5}\\{x-y=0}\end{array}\right.$
解得:$\left\{\begin{array}{l}{{x}_{1}=\frac{10}{3}}\\{{y}_{1}=\frac{5}{3}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=\frac{5}{2}}\\{{y}_{2}=\frac{5}{2}}\end{array}\right.$.
點評 本題考查了二元二次方程組的解法.把二元二次方程組轉化為二元一次是解決本題的關鍵.


科目:初中數學 來源: 題型:解答題
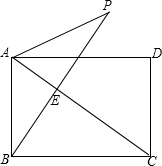 如圖,矩形ABCD中,AB=6,BC=8,過點B作BE⊥AC,垂足為E,把△ABE沿AE翻折,得△APE.
如圖,矩形ABCD中,AB=6,BC=8,過點B作BE⊥AC,垂足為E,把△ABE沿AE翻折,得△APE.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 3.93×105米 | B. | 3.9×105米 | C. | 3.93×104米 | D. | 3.9×104米 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\left\{\begin{array}{l}x=2\\ y=3\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=1\\ y=4\end{array}\right.$ | C. | $\left\{\begin{array}{l}x=3\\ y=2\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=4\\ y=1\end{array}\right.$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
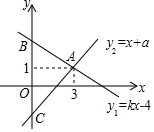 如圖,一次函數y1=kx+4與y2=x+a的圖象相交于點A(3,1),與y軸分別相交于點B、C兩點.
如圖,一次函數y1=kx+4與y2=x+a的圖象相交于點A(3,1),與y軸分別相交于點B、C兩點.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 由向左平移3個單位,再向上平移2個單位 | |
| B. | 由向右平移3個單位,再向下平移2個單位 | |
| C. | 由向右平移3個單位,再向上平移2個單位 | |
| D. | 由向左平移3個單位,再向下平移2個單位 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com