
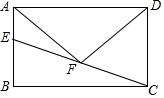
 已知:如圖,在矩形ABCD中,點E在邊AB上,點F為CE的中點,連接AF、DF.
已知:如圖,在矩形ABCD中,點E在邊AB上,點F為CE的中點,連接AF、DF.分析 (1)延長AF交DC延長線于點M,如圖,先根據矩形的性質得到AB∥CD,∠ADC=90°,再利用平行線的性質得∠EAF=∠M,則可根據“ASA”判定△AFM≌△MFC,得到AF=FM,然后利用直角三角形斜邊上的中線性質可判定△AFD為等腰三角形;
(2)設AE=x,△ADF的面積用S表示,利用全等的性質得到CM=AE=x,再根據三角形面積公式得到S△ADF=$\frac{1}{2}$S△ADM=$\frac{1}{2}$•$\frac{1}{2}$•5•(3+x),則x=$\frac{4S-15}{5}$,再利用0<x<3得到0<$\frac{4S-15}{5}$<3,解不等式得到得S的整數值為4、5、6、7,然后分別計算對應的x的值即可.
解答 (1)證明:延長AF交DC延長線于點M,如圖,
∵四邊形ABCD為ABCD,
∴AB∥CD,∠ADC=90°,
∴∠EAF=∠M,
在△AFM和△MFC中
$\left\{\begin{array}{l}{∠EAF=∠M}\\{FE=FC}\\{∠AFE=∠MFC}\end{array}\right.$,
∴△AFM≌△MFC,
∴AF=FM,
∴DF為Rt△ADM的斜邊AM上的中線,
∴AF=DF=MF,
∴△AFD為等腰三角形;
(2)解:設AE=x,△ADF的面積用S表示,
∵△AFM≌△MFC,
∴CM=AE=x,
∵AF=MF,
∴S△ADF=$\frac{1}{2}$S△ADM=$\frac{1}{2}$•$\frac{1}{2}$•5•(3+x),
即S=$\frac{5x+15}{4}$,
∴x=$\frac{4S-15}{5}$,
∵0<x<3,
∴0<$\frac{4S-15}{5}$<3,解得3.75<S<7.5,
∴S的整數值為4、5、6、7,
當S=4時,x=$\frac{4S-15}{5}$=$\frac{1}{5}$,
當S=5時,x=$\frac{4S-15}{5}$=1,
當S=6時,x=$\frac{4S-15}{5}$=$\frac{9}{5}$,
當S=7時,x=$\frac{4S-15}{5}$=$\frac{13}{5}$,
即當△AFD的面積為整數時AE的長為$\frac{1}{5}$,1,$\frac{9}{5}$,$\frac{13}{5}$.
點評 本題考查了矩形的性質:平行四邊形的性質矩形都具有;矩形的四個角都是直角.也考查了全等三角形的判定與性質.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
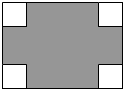 在長為8cm、寬為5cm的矩形的四個角上分別截去四個全等的小正方形,使得留下的圖形(圖中陰影部分)面積是原矩形面積的80%,求所截去小正方形的邊長.
在長為8cm、寬為5cm的矩形的四個角上分別截去四個全等的小正方形,使得留下的圖形(圖中陰影部分)面積是原矩形面積的80%,求所截去小正方形的邊長.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
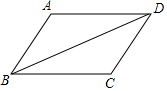 如圖:請在下列四個條件:①AD∥BC,②AB=CD,③∠A=∠C,④AB∥CD中,選出兩個,能推出△ABD≌△CDB:①②.(只要寫出正確的一種即可)
如圖:請在下列四個條件:①AD∥BC,②AB=CD,③∠A=∠C,④AB∥CD中,選出兩個,能推出△ABD≌△CDB:①②.(只要寫出正確的一種即可)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 銷售量x(千克) | 銷售價c(元) |
| 1 | 2+0.1 |
| 2 | 4+0.2 |
| 3 | 6+0.3 |
| 4 | 8+0.4 |
| … | … |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 將連續的奇數1,3,5,7,9…,排成如下的數表:
將連續的奇數1,3,5,7,9…,排成如下的數表:查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com