
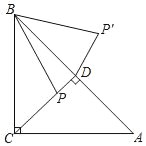
【題目】如圖,在△ABC中,∠ACB=90°,AC=BC=4,P是△ABC的高CD上一個動點,以B點為旋轉中心把線段BP逆時針旋轉45°得到BP′,連接DP′,則DP′的最小值是( )
A.2![]() -2B.4﹣2
-2B.4﹣2![]() C.2﹣
C.2﹣![]() D.
D.![]() -1
-1
【答案】A
【解析】
在BC上截取BE=BD,根據等腰直角三角形的性質求得BA和BE,再由旋轉的性質證明△BDP'≌△BEP,從而可得到PE=P'D,再由等腰直角三角形的性質求得PE,從而求得DP′的最小值.
解:如圖,在BC上截取BE=BD,
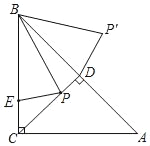
∵∠ACB=90°,AC=BC=4, CD⊥AB,
∴BA=4![]() ,∠ABC=∠BAC=∠BCD=∠DCA=45°,BD=CD=AD=2
,∠ABC=∠BAC=∠BCD=∠DCA=45°,BD=CD=AD=2![]() =BE,
=BE,
∵旋轉
∴BP=BP',∠PBP'=45°,
∵BE=BD,∠ABC=∠PBP'=45°,BP=BP'
∴△BDP'≌△BEP(SAS)
∴PE=P'D
∴當PE⊥CD時,PE有最小值,即DP'有最小值,
∵PE⊥CD,∠BCD=45°,
∴CE=![]() PE=BC﹣BE=4﹣2
PE=BC﹣BE=4﹣2![]()
∴P'D =PE=2![]() ﹣2
﹣2
故選:A.


科目:初中數學 來源: 題型:
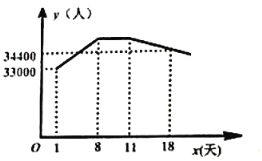
【題目】某市植物園于2019年3月-5月舉辦花展,按照往年的規律推算,自4月下旬起游客量每天增加![]() 人,游客量預計將在5月1日達到高峰,并持續到5月4日,隨后游客量每天有所減少.已知4月24日為第一天起,每天的游客量
人,游客量預計將在5月1日達到高峰,并持續到5月4日,隨后游客量每天有所減少.已知4月24日為第一天起,每天的游客量![]() (人)與時間
(人)與時間![]() (天)的函數圖像如圖所示,結合圖像提供的信息,解答下列問題:
(天)的函數圖像如圖所示,結合圖像提供的信息,解答下列問題:
![]() 已知該植物園門票
已知該植物園門票![]() 元/張,若每位游客在園內每天平均消費
元/張,若每位游客在園內每天平均消費![]() 元,試求5月1日-5月4日,所有游客消費總額為多少元?
元,試求5月1日-5月4日,所有游客消費總額為多少元?
![]() 當
當![]() 時,求
時,求![]() 關于
關于![]() 的函數解析式.
的函數解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形![]() 中,
中,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點,連接
的中點,連接![]() ,
,![]() ,交點為
,交點為![]() . 若正方形的邊長為
. 若正方形的邊長為![]() .
.
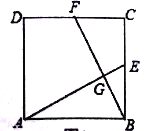
(1)求證:![]() ;
;
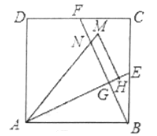
(2)將![]() 沿
沿![]() 對折,得到
對折,得到![]() (如圖),延長
(如圖),延長![]() 交
交![]() 的延長線于點
的延長線于點![]() ,求
,求![]() 的長;
的長;
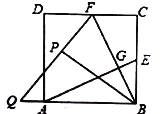
(3)將![]() 繞點
繞點![]() 逆時針方向旋轉,使邊
逆時針方向旋轉,使邊![]() 正好落在
正好落在![]() 上,得到
上,得到![]() (如圖),若
(如圖),若![]() 和
和![]() 相交于點
相交于點![]() ,求四邊形
,求四邊形![]() 面積.
面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
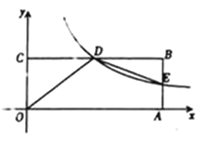
【題目】如圖,在平面直角坐標系![]() 中,矩形
中,矩形![]() 的頂點
的頂點![]() 在
在![]() 軸上,頂點
軸上,頂點![]() 在
在![]() 軸上,
軸上,![]() 是
是![]() 的中點,過點
的中點,過點![]() 的反比例函數圖象交
的反比例函數圖象交![]() 于點
于點![]() ,連接
,連接![]() ,若
,若![]() .
.
![]() 求過點
求過點![]() 的反比例函數的解析式及
的反比例函數的解析式及![]() 所在直線的函數解析式.
所在直線的函數解析式.
![]() 設直線
設直線![]() 與
與![]() 軸和
軸和![]() 軸的交點分別為
軸的交點分別為![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A1、A2、A3…在直線y=x上,點C1,C2,C3…在直線y=2x上,以它們為頂點依次構造第一個正方形A1C1A2B1,第二個正方形A2C2A3B2…,若A2的橫坐標是1,則B3的坐標是_____,第n個正方形的面積是_____.
[Failed to download image : http://192.168.0.10:8086/QBM/2019/5/21/2208296361205760/2209339150704640/STEM/947823175bfc4b878475a9a15e16a258.png]
查看答案和解析>>
科目:初中數學 來源: 題型:
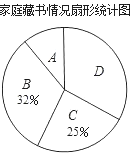
【題目】在“書香校園”活動中,某校為了解學生家庭藏書情況,隨機抽取本校部分學生進行調查,并繪制成部分統計圖表如下:
類別 | 家庭藏書m本 | 學生人數 |
A | 0≤m≤25 | 20 |
B | 26≤m≤100 | a |
C | 101≤m≤200 | 50 |
D | m≥201 | 66 |
根據以上信息,解答下列問題:
(1)該調查的樣本容量為_____,a=_____;
(2)在扇形統計圖中,“A”對應扇形的圓心角為_____°;
(3)若該校有2000名學生,請估計全校學生中家庭藏書200本以上的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的邊長是2,點E是CD邊的中點,點F是邊BC上不與點B,C重合的一個動點,把∠C沿直線EF折疊,使點C落在點C′處.當△ADC′為等腰三角形時,FC的長為_____.
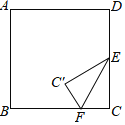
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,B(2m,0)、C(3m,0)是平面直角坐標系中兩點,其中m為常數,且m>0,E(0,n)為y軸上一動點,以BC為邊在x軸上方作矩形ABCD,使AB=2BC,畫射線OA,把△ADC繞點C逆時針旋轉90°得△A′D′C′,連接ED′,拋物線y=ax2+bx+n(a≠0)過E、A′兩點.
(1)填空:∠AOB= °,用m表示點A′的坐標:A′ ;
(2)當拋物線的頂點為A′,拋物線與線段AB交于點P,且![]() 時,△D′OE與△ABC是否相似?說明理由;
時,△D′OE與△ABC是否相似?說明理由;
(3)若E與原點O重合,拋物線與射線OA的另一個交點為M,過M作MN垂直y軸,垂足為N:
①求a、b、m滿足的關系式;
②當m為定值,拋物線與四邊形ABCD有公共點,線段MN的最大值為5,請你探究a的取值范圍.
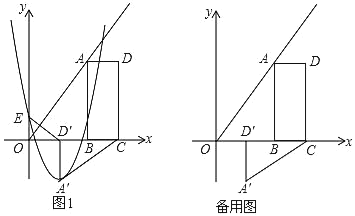
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,按以下步驟作圖:
,按以下步驟作圖:
①:以點![]() 為圓心,以小于
為圓心,以小于![]() 的長為半徑畫弧,分別交
的長為半徑畫弧,分別交![]() 、
、![]() 于點
于點![]() 、
、![]() ;
;
②:分別以點![]() 、
、![]() 為圓心,以大于
為圓心,以大于![]() 的長為半徑畫弧,兩弧相交于點
的長為半徑畫弧,兩弧相交于點![]() ;
;
③:作射線![]() ,交
,交![]() 邊于點
邊于點![]() ,
,
若![]() ,
,![]() ,則
,則![]() ( )
( )
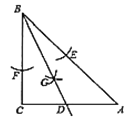
A. 3B. ![]() C. 6D.
C. 6D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com