
 如圖,點O是等邊△ABC內一點,∠AOB=110°,∠BOC=α,將△BOC繞點C順時針方向旋轉60°,到△ADC,連接OD.
如圖,點O是等邊△ABC內一點,∠AOB=110°,∠BOC=α,將△BOC繞點C順時針方向旋轉60°,到△ADC,連接OD.分析 (1)由旋轉的性質得出CO=CD,∠OCD=60°,即可得出結論;
(2)由旋轉的性質得出△BOC≌△ADC,得出∠ADC=∠BOC=150°,由等邊三角形的性質得出∠ODC=60°,求出∠ADO=90°即可;
(3)分三種情況:①AO=AD時;②OA=OD時;③OD=AD時;由等腰三角形的性質和三角形內角和定理即可求出結果.
解答 (1)證明:由旋轉的性質得:CO=CD,∠OCD=60°,
∴△COD是等邊三角形;
(2)解:當α=150°,即∠BOC=150°時,△AOD是直角三角形.理由如下:
由旋轉的性質得:△BOC≌△ADC,
∴∠ADC=∠BOC=150°,
又∵△COD是等邊三角形,
∴∠ODC=60°,
∴∠ADO=90°,
即△AOD是直角三角形;
(3)解:分三種情況:
①AO=AD時,∠AOD=∠ADO.
∵∠AOD=360°-∠AOB-∠COD-α=360°-110°-60°-α=190°-α,∠ADO=α-60°,
∴190°-α=α-60°
∴α=125°;
②OA=OD時,∠OAD=∠ADO.
∵∠AOD=190°-α,∠ADO=α-60°,
∴∠OAD=180°-(∠AOD+∠ADO)=50°,
∴α-60°=50°
∴α=110°;
③OD=AD時,∠OAD=∠AOD.
∵190°-α=50°
∴α=140°.
綜上所述:當α的度數為125°或110°或140°時,△AOD是等腰三角形.(
點評 本題是三角形綜合題目,以“空間與圖形”中的核心知識(如等邊三角形的性質、全等三角形的性質與證明、直角三角形的判定、多邊形內角和等)為載體,內容由淺入深,層層遞進.試題中幾何演繹推理的難度適宜,蘊含著豐富的思想方法(如運動變化、數形結合、分類討論、方程思想等),能較好地考查學生的推理、探究及解決問題的能力.


科目:初中數學 來源: 題型:解答題
 如圖①,已知△ABC是等腰三角形,∠BAC=90°,點D是BC的中點,作正方形DEFG,使點A、C分別在DG和DE上,連接AE、BG.
如圖①,已知△ABC是等腰三角形,∠BAC=90°,點D是BC的中點,作正方形DEFG,使點A、C分別在DG和DE上,連接AE、BG.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知拋物線l1經過原點與A點,其頂點是P(-2,3),平行于y軸的直線m與x軸交于點B(b,0),與拋物線l1交于點M.
如圖,已知拋物線l1經過原點與A點,其頂點是P(-2,3),平行于y軸的直線m與x軸交于點B(b,0),與拋物線l1交于點M.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,(1)a<0 (2)b>0
已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,(1)a<0 (2)b>0| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,扇形OAB上有一動點P,P從點A出發,沿$\widehat{AB}$、線段BO、線段OA勻速運動到點A,則OP的長度y與運動時間t之間的函數圖象大致是 ( )
如圖,扇形OAB上有一動點P,P從點A出發,沿$\widehat{AB}$、線段BO、線段OA勻速運動到點A,則OP的長度y與運動時間t之間的函數圖象大致是 ( )| A. |  | B. |  | C. | 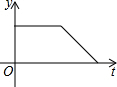 | D. |  |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
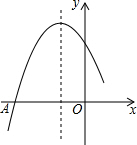 如圖是二次函數y=ax2+bx+c圖象的一部分,圖象過點A(-3,0),對稱軸為直線x=-1,給出四個結論,其中正確結論是( )
如圖是二次函數y=ax2+bx+c圖象的一部分,圖象過點A(-3,0),對稱軸為直線x=-1,給出四個結論,其中正確結論是( )| A. | b2<4ac | |
| B. | 2a+b=0 | |
| C. | a+b+c>0 | |
| D. | 若點B($\frac{5}{2}$,y1)、C($\frac{1}{2}$,y2)為函數圖象上的兩點,則y1<y2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com