
分析 根據每層第一個數以及該層數的個數即可得出第n層第一個數為n2,共n+1個數,令n2≤2510<(n+1)2結合n為正整數即可求出n的值,再用2510-n2+1即可得出該數為第幾個,此題得解.
解答 解:∵第1層第一個數為1,共2個數;第2層第一個數為4,共3個數;第3層第一個數為9,共4個數;第4層第一個數為16,共5個數;…,
∴第n層第一個數為n2,共n+1個數.
令n2≤2510<(n+1)2,n為正整數,
解得:n=50,
∵2510-2500+1=11,
∴2510為第50層第11個數.
故答案為:50;11.
點評 本題考查了規律型中數字的變化類,根據每層第一個數以及該層數的個數的變化找出變化規律是解題的關鍵.


科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
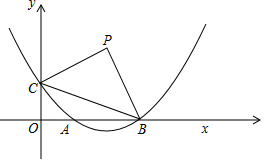 已知:如圖,在平面直角坐標系xOy中,拋物線y=ax2-4ax+1與x軸的正半軸交于點A和點B,與y軸交于點C,且OB=3OC,點P是第一象限內的點,連接BC,△PBC是以BC為斜邊的等腰直角三角形.
已知:如圖,在平面直角坐標系xOy中,拋物線y=ax2-4ax+1與x軸的正半軸交于點A和點B,與y軸交于點C,且OB=3OC,點P是第一象限內的點,連接BC,△PBC是以BC為斜邊的等腰直角三角形.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
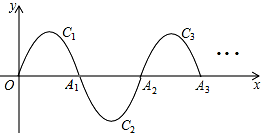 如圖,一條拋物線y=-x(x-2)(0≤x≤2)的一部分,記為C1,它與x軸交于O,A1兩點,將C1繞點A1旋轉180°得到C2,交x軸于點A2,;將C2繞點A2旋轉180°得到C3,交x軸于A3;…如此進行下去,直至得到C6,若點P(2017,y)在拋物線Cn上,則y=1.
如圖,一條拋物線y=-x(x-2)(0≤x≤2)的一部分,記為C1,它與x軸交于O,A1兩點,將C1繞點A1旋轉180°得到C2,交x軸于點A2,;將C2繞點A2旋轉180°得到C3,交x軸于A3;…如此進行下去,直至得到C6,若點P(2017,y)在拋物線Cn上,則y=1.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com