Question

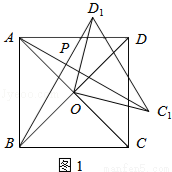
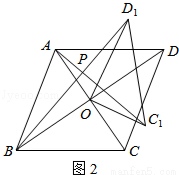
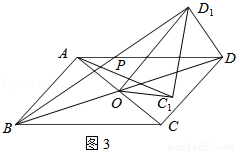
在四邊形ABCD中，對角線AC、BD相交于點O，將△COD繞點O按逆時針方向旋轉得到△C1OD1，旋轉角為θ（0°＜θ＜90°），連接AC1、BD1，AC1與BD1交于點P．

（1）如圖1，若四邊形ABCD是正方形．

①求證：△AOC1≌△BOD1．

②請直接寫出AC1 與BD1的位置關系．

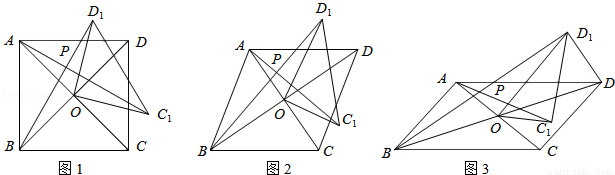
（2）如圖2，若四邊形ABCD是菱形，AC=5，BD=7，設AC1=kBD1．判斷AC1與BD1的位置關系，說明理由，并求出k的值．

（3）如圖3，若四邊形ABCD是平行四邊形，AC=5，BD=10，連接DD1，設AC1=kBD1．請直接寫出k的值和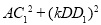的值．

Answer 1

（1）①證明見試題解析；②垂直；（2）AC1⊥BD1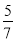，；（3）25．

【解析】

試題分析：（1）①如圖1，根據正方形的性質得OC=OA=OD=OB，AC⊥BD，則∠AOB=∠COD=90°，再根據旋轉的性質得OC1=OC，OD1=OD，∠COC1=∠DOD1，則OC1=OD1，利用等角的補角相等得∠AOC1=∠BOD1，然后根據“SAS”可證明△AOC1≌△BOD1；

②由∠AOB=90°，則∠OAB+∠ABP+∠OBD1=90°，所以∠OAB+∠ABP+∠OAC1=90°，則∠APB=90°所以AC1⊥BD1；

（2）如圖2，根據菱形的性質得OC=OA=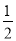AC，OD=OB=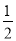BD，AC⊥BD，則∠AOB=∠COD=90°，再根據旋轉的性質得OC1=OC，OD1=OD，∠COC1=∠DOD1，則OC1=OA，OD1=OB，利用等角的補角相等得∠AOC1=∠BOD1，加上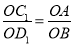，根據相似三角形的判定方法得到△AOC1∽△BOD1，得到∠OAC1=∠OBD1，由∠AOB=90°得∠OAB+∠ABP+∠OBD1=90°，則∠OAB+∠ABP+∠OAC1=90°，則∠APB=90°，所以AC1⊥BD1；然后根據相似比得到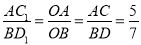，所以；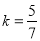

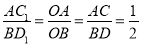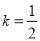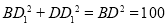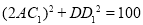（3）與（2）一樣可證明△AOC1∽△BOD1，則，所以；根據旋轉的性質得OD1=OD，根據平行四邊形的性質得OD=OB，則OD1=OB=OD，于是可判斷△BDD1為直角三角形，根據勾股定理得，所以，于是有．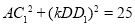

試題解析：（1）①如圖1，∵四邊形ABCD是正方形，∴OC=OA=OD=OB，AC⊥BD，∴∠AOB=∠COD=90°，∵△COD繞點O按逆時針方向旋轉得到△C1OD1，∴OC1=OC，OD1=OD，∠COC1=∠DOD1，∴OC1=OD1，∠AOC1=∠BOD1=90°+∠AOD1，在△AOC1和△BOD1中，∵OA=OB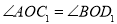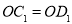，，，∴△AOC1≌△BOD1；

②AC1⊥BD1；

（2）AC1⊥BD1．理由如下：如圖2，∵四邊形ABCD是菱形，∴OC=OA=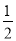AC，OD=OB=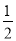BD，AC⊥BD，∴∠AOB=∠COD=90°，∵△COD繞點O按逆時針方向旋轉得到△C1OD1，∴OC1=OC，OD1=OD，∠COC1=∠DOD1，∴OC1=OA，OD1=OB，∠AOC1=∠BOD1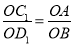，∴，∴△AOC1∽△BOD1，∴∠OAC1=∠OBD1，又∵∠AOB=90°，∴∠OAB+∠ABP+∠OBD1=90°，∴∠OAB+∠ABP+∠OAC1=90°，∴∠APB=90°，∴AC1⊥BD1；∵△AOC1∽△BOD1，∴，∴；

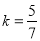（3）如圖3，與（2）一樣可證明△AOC1∽△BOD1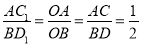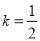，∴，∴；∵△COD繞點O按逆時針方向旋轉得到△C1OD1，∴OD1=OD，而OD=OB，∴OD1=OB=OD，∴△BDD1為直角三角形，在Rt△BDD1中，，∴，∴．

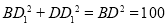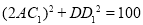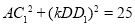考點：1．四邊形綜合題；2．全等三角形的判定與性質；3．旋轉的性質；4．相似三角形的判定與性質．