
已知:如圖,在四邊形ABCD中,AB=AD=8,∠A=60°,∠D=150°,四邊形的周長為32,求BC和DC的長.

10
【解析】
試題分析:連接BD,根據等邊三角形的判定得到△ABD是等邊三角形,相應可求得∠ADB=60°,然后根據等量代換可得∠CDB=90°,即△BDC是直角三角形,再根據四邊形的周長求得BC+CD=16,設CD=x,相應可知BC=16-x,然后根據勾股定理可求得BC的長.
試題解析:【解析】
連接BD
∵AB=AD,∠A=60°,
∴△ABD是等邊三角形.
∴∠ADB=60°.
∵∠ADC=150°,
∴∠CDB=90°
∵AD=8,四邊形的周長為32,
∴BC+CD=16
設CD=x.則BC=16-x.
根據勾股定理
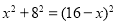
解得x=6 .
∴CD=6.
∴BC=10
考點:等邊三角形,直角三角形的判定,勾股定理


 寒假學與練系列答案
寒假學與練系列答案科目:初中數學 來源:2014-2015學年北京市東城區九年級上學期期末考試數學試卷(解析版) 題型:解答題
在四邊形ABCD中,對角線AC、BD相交于點O,將△COD繞點O按逆時針方向旋轉得到△C1OD1,旋轉角為θ(0°<θ<90°),連接AC1、BD1,AC1與BD1交于點P.
(1)如圖1,若四邊形ABCD是正方形.
①求證:△AOC1≌△BOD1.
②請直接寫出AC1 與BD1的位置關系.
(2)如圖2,若四邊形ABCD是菱形,AC=5,BD=7,設AC1=kBD1.判斷AC1與BD1的位置關系,說明理由,并求出k的值.
(3)如圖3,若四邊形ABCD是平行四邊形,AC=5,BD=10,連接DD1,設AC1=kBD1.請直接寫出k的值和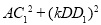 的值.
的值.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年北京市東城區九年級上學期期末考試數學試卷(解析版) 題型:選擇題
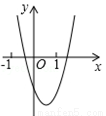
已知二次函數 (a,b,c是常數,且
(a,b,c是常數,且 )的圖象如圖所示,則一次函數
)的圖象如圖所示,則一次函數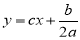 與反比例函數
與反比例函數 在同一坐標系內的圖象大致是( )
在同一坐標系內的圖象大致是( )
A. B.
B.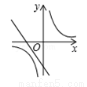 C.
C. D.
D.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年北京市大興區九年級上學期期末考試數學試卷(解析版) 題型:解答題
如圖,在平面直角坐標系中,以點C(1,1)為圓心,2為半徑作圓,交 軸
軸
于 兩點,點
兩點,點 在⊙
在⊙ 上.
上.

(1)求出 兩點的坐標;
兩點的坐標;
(2)試確定經過A、B且以點P為頂點的拋物線解析式;
(3)在該拋物線上是否存在一點 ,使線段
,使線段 與
與 互相平分?若存在,求出點
互相平分?若存在,求出點 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年北京市大興區九年級上學期期末考試數學試卷(解析版) 題型:解答題
已知:如圖,一次函數 的圖象與反比例函數
的圖象與反比例函數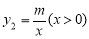 的圖象交于A(1,6),B(
的圖象交于A(1,6),B(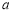 ,2)兩點.
,2)兩點.
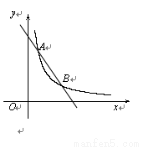
(1)求一次函數與反比例函數的表達式;
(2)直接寫出 ≥
≥ 時
時 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年北京市大興區九年級上學期期末考試數學試卷(解析版) 題型:選擇題
已知拋物線y=ax2+bx和直線y=ax+b在同一坐標系內的圖象如圖,其中正確的是( )
A.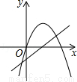 B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年北京市朝陽區九年級上學期期末考試數學試卷(解析版) 題型:解答題
如圖,在平面直角坐標系xOy中,以點A(2,3)為圓心的⊙A交 x軸于點B,C,BC=8,求⊙A的半徑.

查看答案和解析>>
科目:初中數學 來源:2014-2015學年重慶市七年級上學期期末考試數學試卷(解析版) 題型:解答題
某品牌汽車生產廠為了占領市場提高銷售量,對經銷商采取銷售獎勵活動,在2014年10月前獎勵辦法以下表計算獎勵金額,2014年10月后以新獎勵辦法執行.某經銷商在新獎勵辦法出臺前一個月共售出某品牌汽車的A型和B型共413臺,新獎勵辦法出臺后的第一個月售出這兩種型號的汽車共510臺,其中A型和B型汽車的銷售量分別比新獎勵辦法出臺前一個月增長25%和20%.2014年10月前獎勵辦法:
銷售量(x臺) | 每臺獎勵金額(元) |
0<x≤ 100 | 200 |
100<x≤300 | 500 |
x>300 | 1000 |
(1)在新辦法出臺前一個月,該經銷商共獲得獎勵金額多少元?
(2)在新辦法出臺前一個月,該經銷商銷售的A型和B型汽車分別為多少臺?
(3)若A型汽車每臺售價為10萬元,B型汽車每臺售價為12萬元.新獎勵辦法是:每銷售一臺A型汽車按每臺汽車售價的 給予獎勵,每銷售一臺B型汽車按每臺汽車售價的
給予獎勵,每銷售一臺B型汽車按每臺汽車售價的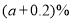 給予獎勵.新獎勵辦法出臺后的第二個月,A型汽車的銷售量比出臺后的第一個月增加了
給予獎勵.新獎勵辦法出臺后的第二個月,A型汽車的銷售量比出臺后的第一個月增加了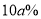 ; 而B型汽車受到某問題零件召回的影響,銷售量比出臺后的第一個月減少了
; 而B型汽車受到某問題零件召回的影響,銷售量比出臺后的第一個月減少了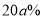 ,新獎勵辦法出臺后的第二個月該經銷商共獲得的獎勵金額355680元,求
,新獎勵辦法出臺后的第二個月該經銷商共獲得的獎勵金額355680元,求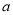 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com